[vgwort line=“90″ server=“vg05″ openid=“5675208fa34b4c159a0a4ca8d68a622b“]
Nein, natürlich nicht!
Aber die Anhänger der flachen Erde versuchen gerne im Grenzbereiche ihrer Messinstrumente zu beweisen, dass die Erde nicht rund sein kann, weil sie keine Krümmung sehen können. Etwas nicht sehen zu können, bedeutet jedoch nicht, dass es nicht da ist. Mein Schlafzimmerschrank ist auch nicht weg, weil ich ihn mitten in der Nacht nicht sehe. Dass wir im Alltag keine Krümmung der Erde sehen, liegt jedoch nur daran, dass wir nicht genau genug hinschauen. Dies möchte ich mit einer Handwerkerwasserwaage verdeutlichen
Die folgende Skizze zeigt die Berechnung der Neigung der Linie Auge – Horizont auf einer kugelförmigen Erde gegenüber der Waagerechten. Die beiden Linien am unteren Rand zeigen dies etwa maßstabsgerecht für etwa 5 m Augeshöhe auf 20 cm. (Leider ist Genauigkeit von LibrOffice etwas beschränkt.) Wie sie sehen, können Sie keine zwei Linien unterscheiden. Die Auflösung der Skizze ist zu schlecht.
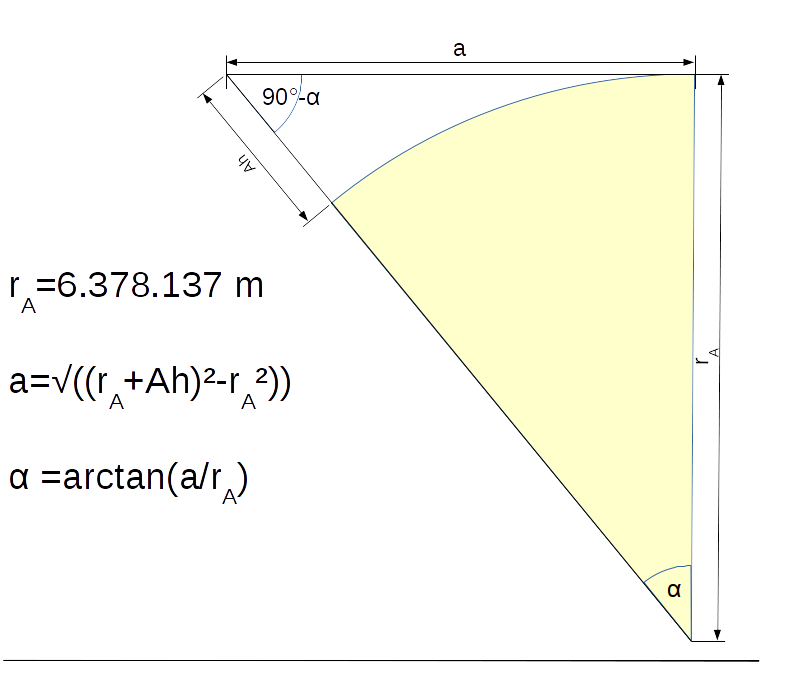
Nehmen wir einmal an, wir stehen am Meer auf 5 Meter Augeshöhe. Dann ist der Horizont gemäß der Theorie einer Kugelförmigen Erde etwa 8 km entfernt. Genauer:
| Punk A | ||
| Radius RA | 6.378.137,00 | m |
| Augeshöhe Ah | 5,00 | m |
| Punkt bis Horizont | 7.986,33 | m |
| Entfernung A-B | 8.000,00 | m |
| Neigungswinkel | 0,0012521 | rad |
| Neigungswinkel | 0,0717423 | ° |
Der Winkel des rechtwinkligen Dreiecks zwischen Standpunkt und Horizontpunkt beträgt etwa 0,07° oder 4,3′(Bogenminuten). Am Standpunkt neigt sich die „Ebene“ also nur 0,07°. Dies ist etwa ein Siebtel des scheinbaren Durchmessers der Sonne. So kleine Winkel lassen sich auch mit einem sehr guten Sextanten (Genauigkeit 10 bis 20 Bogensekunden) nur auf ungefähr 5% genau messen.
Übertragen wir diese Verhältnisse auf eine 800 mm lange Wasserwaage, dann bedeutet dies, dass wir die Wasserwaage auf einer Seite um einen Millimeter anheben müssen um den Unterschied maßstabsgerecht zu verdeutlichen.
| Wasserwaage | ||
| Länge | 0,8000 | m |
| Gegenkathete | 0,0010 | m |
| Winkel | 0,0013 | rad |
| Winkel | 0,0716 | ° |
Ohne die Hilfe der Libelle ist der Unterschied mit bloßem Auge kaum zu erkennen. Wenn Sie dies könnten, bräuchten Sie keine Wasserwaage. Und auch mit Libelle müssen Sie sehr genau hinsehen, um den Unterschied festzustellen: Dies zeigen die folgenden beiden Fotos.

Frei stehend, mit Blick auf den Horizont ist die Krümmung der Erde mit dem bloßem Auge – ohne technische Hilfsmittel – auf geringen Augeshöhen nicht wahrnehmbar. Erst auf 250 m Augeshöhe beträgt der Neigungswinkel ungefähr ein halbes Grad, was der scheinbaren Größe der Sonne entspricht. Erst 1.000 m Höhe steigt der Neigungswinkel auf ~1°; auch dieser Winkel lässt sich auch nicht mal eben mit einem an den Horizont gehaltenen Lineal oder Geodreieck messen. Selbst auf dem Mt Everest beträgt der Neigungswinkel in 8848 m Höhe nur 3°.
Fazit: Die Krümmung sieht man nicht, weil sie zu gering ist, um ohne technische Hilfsmittel gesehen zu werden.
Am Tag der Sonnenwende im Juni oder Dezember könnte man den Abstand der Sonne zur flachen Erde mit einfachen Mitteln bestimmen. In diesem Fall wird man jedoch widersprüchliche Abstände feststellen, die nur auflösbar sind, wenn die Erde eine Kugel ist.


Neueste Kommentare