Ist die Erde flach? (Teil 5)

[vgwort line=“91″ server=“vg05″ openid=“59b1eca7183843c895f35f7bce03c03f“]
Nein, natürlich nicht!

Um die flache Erde mit den Beobachtungen in Einklang zu bringen werden die verschiedensten Modelle ins Spiel gebracht. Alle haben jedoch einen Haken: Im Gegensatz zu den Modellen der runden oder gekrümmten Erde gibt es kein mathematischen Modell, das mit den Beobachtungen in Einklang zu bringen ist.

Nehmen wir an die Erde wäre flach.

Höhe der Sonne über der flachen Erde

Nehmen wir als Beispiel die Höhe der Sonne über einer flachen Erde. Gerne wird behauptet, dass die Sonne kleiner ist als behauptet und auch viel näher dran steht. Außerdem sei sie nicht rund, und so weiter und so fort. Die Frage, die sich hier stellt, lautet: Wie weit ist die Sonne – zu einem bestimmten Zeitpunkt – von der flachen Erde entfernt?

Nehmen wir dazu einen der beiden Tage der „Tagundnachtgleiche„. An diesem Tag scheint die Sonne 12 Stunden und 12 Stunden ist es dunkel. Die Sonne steht zur Mittagszeit senkrecht über dem Äquator und exakt im Süden oder Norden, je nachdem, ob wir uns nördlich oder südlich es Äquators befinden. Je weiter man nach Norden kommt, desto niedriger steht sie über dem Horizont. Der Winkel über dem Horizont beträgt 90 Grad minus die geografische Breite. Wir wollen die Höhe der Sonne über der flachen Erde für drei spezielle ausgewählte Orts aussuchen. Dies sind 30°, 45° und 60° südlicher und nördlicher Breite. Diese Orte haben den Vorteil, dass wir auf trigonometrische Funktionen bei der Berechnung verzichten können.

Die notwendigen Beobachtungen lassen sind im Prinzip ohne großen Aufwand von jedem mit einem Stab, einer Wasserwaage und einem Maßband mit einer hinreichenden Messgenauigkeit durchführen.

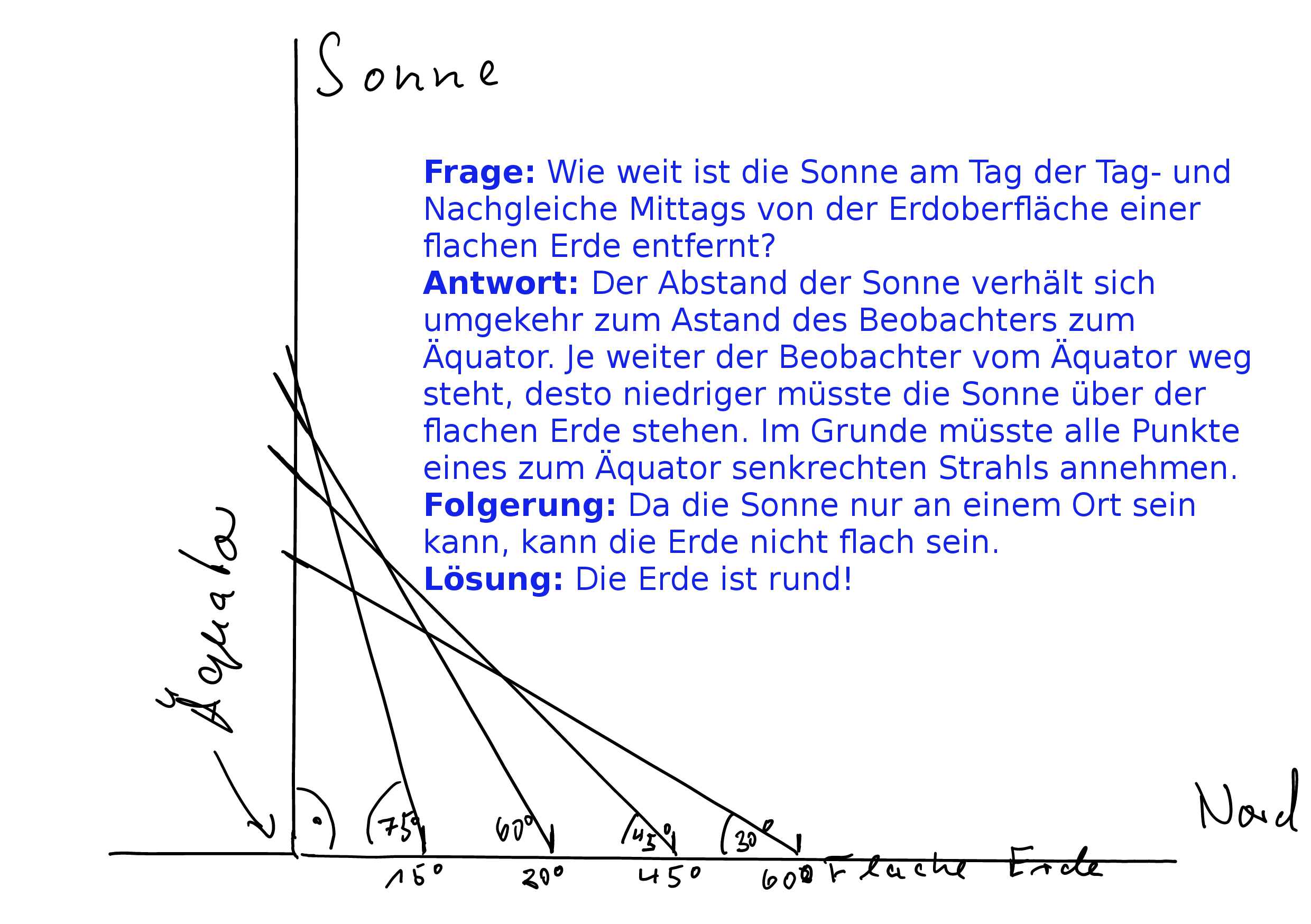
Auf 30° nördlicher oder südlicher Breite steht die Sonne am Tag der Tagundnachtgleiche 60° über dem Horizont. (Wer es nicht glaubt, kann es man 21.3. oder 23.9. eines Jahres nachprüfen.) Der Abstand zwischen 30° Süd und 30° Nord sei a. (Auf einer Kugel wäre dieser Abstand a = r * π / 3. Auf der Erde mit r = 6.378,137 km somit 6.679,169 km ). Zwischen dem südlichem und nördlichen Beobachter und der Sonne bildet sich ein gleichseitiges und -winkliges Dreieck. Die Höhe der Sonne ist damit h = (Sqrt(3) * a) / 2 = 0,866 * a. (Wer es nicht glaubt, darf es gern mit dem Pythagoras jeweils selbst herleiten.)

Auf 45° nördlicher oder südlicher Breite steht die Sonne 45° über dem Horizont. Dies ergibt ein gleichseitiges Dreieck mit zwei 45° Winkeln. In diesem Dreieck ist die Sonnenhöhe gleich dem Abstand des Beobachters zum Äquator. Der Abstand zwischen 45° Süd und 45° Nord ist anderthalb mal größer als der zwischen 30° Süd und Nord. Er ist somit 1,5 * a. Für die Höhe der Sonne ergibt sich somit h = (3/4) * a = 0,75 * a. Da ist nun ziemlich weit von unserem ersten Ergebnis h = (Sqrt(3) * a) / 2 = 0,866 * a entfernt.

Auf 60° nördlicher oder südlicher Breite steht die Sonne also 30° über dem Horizont. Auch hier ergibt sich ein gleichseitiges und -winkliges Dreieck mit der doppelten Sonnenhöhe als Seitenlänge. In diesem Fall ist die Höhe der Sonne h = a / Sqrt(3) = 0,577 a. Auch dies Ergebnis weicht erheblich von den beiden anderen Ergebnissen ab.

Übertragen einen Tabelle mit den Entfernungen auf der flachen oder runden Erde bedeutet dies:

	Abstand Süd – Nord	Sonnenhöhe	Einheit
30°	6.679.169,45	5.784.330,42	m
45°	10.018.754,17	5.009.377,09	m
60°	13.358.338,90	3.856.220,28	m
Erdradius rA	6.378.137,00		m

BTW: Für den Nord- oder Südpol ergibt sich eine Höhe von 0.

Schauen wir uns an, was passiert, wenn wir die Höhe der Sonne anhand der Positionen 60° Süd und 30° Nord bestimmen wollen. (Wir könnten auch 30° Nord und 60° Nord nehmen, das Ergebnis wäre identisch.)

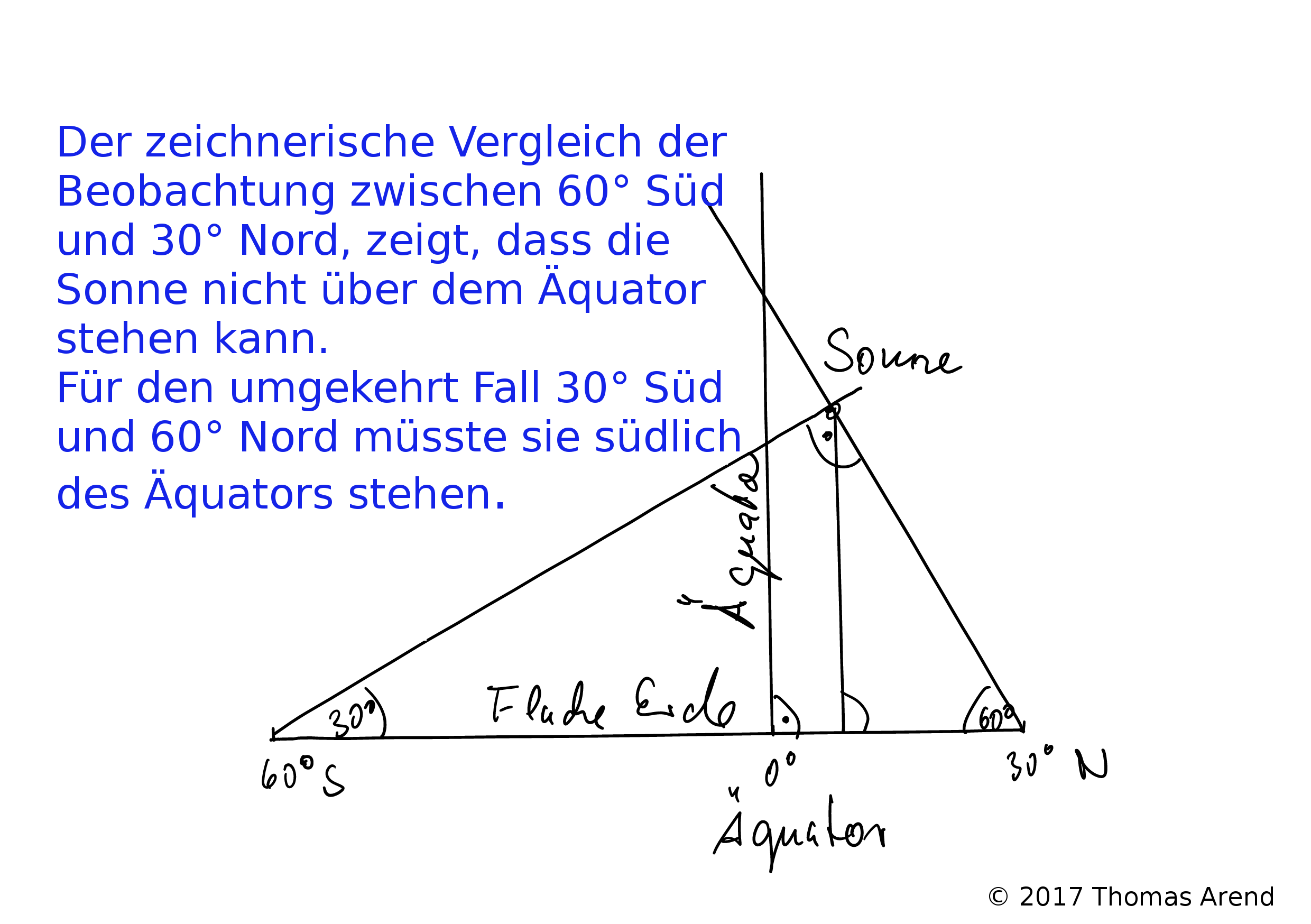
In diesem Fall steht die Sonne nicht mehr über den Äquator, was aber Voraussetzung für einen Tag der Tagundnachtgleiche ist. Mit sin(30°) = 0,5 ergibt sich: a (0,5 – 1,5 * 0,5 * 0,5) = 0,125 * a. Dies entspräche 7,5° Nord. Tauschen wir Nord und Süd, dann steht die Sonne auf 7,5° Süd. Dies widerspricht der Beobachtung, dass sie über dem Äquator steht allerdings erheblich.

Nicht nur die Höhe der Sonne, sondern auch ihr Punkt über der flachen Erde ändert sich mit den Beobachtungsorten. Für zwei beliebige Paare von Beobachtungsorten steht die Sonne an einem anderen Ort.

Fazit

Das Modell der flachen Erde ist mit den Beobachtungen nicht vereinbar. Sowohl die Höhe der Sonne als auch ihre Position über einer flachen Erde kann sich nicht mit dem Ort des Beobachters ändern. Da diese ein Widerspruch zur Annahme eienr flachen Erde ist, ergibt sich, dass Annahme der flachen Erde falsch ist.

Die Erde muss rund sein.

Wie man sieht, ist der Beweis einer runden, gekrümmten Erde recht simpel. Man muss dazu nicht versuchen die Krümmung des Plattensees auf 6km zu messen. BTW: Der See ist über 70 km lang. Da hätte man vielleicht die Längsseite nehmen sollen.