[vgwort line=“89″ server=“vg05″ openid=“010bc25822434f45b73f074253ecb2ac“]
Nein, natürlich nicht! Aber immer wieder „beweisen“ Anhänger der Theorie der flache Erde, dass die Erde flach ist. Da sie aber mehr oder weniger eine Kugel ist, müssen diese „Beweise“ falsch sein. Aber wo liegt der oder die Fehler in den einzelnen Beweisen. Vor ein paar Tagen bin ich auf den Artikel Euronia.com – Die Erde ist flach gestoßen. Hier wird versucht die flache Erde am Bodensee mit dem Bild der Schlosskirch Friedrichshafen zu beweisen. Nur das Bild beweist genau das Gegenteil, die Erde ist rund.
Schauen wir uns die Schlosskirche an. Die Kirche liegt nicht direkt am Ufer, sondern auf einem Hügel. Die Türme sind laut www.schlosskirche-fn.de 54,9 Meter hoch. Wie hoch die Kirche liegt, konnte ich leider nicht herausfinden. Sie sind in drei gut unterscheidbare Abschnitte und das Zwiebeldach geteilt.
Auf alle Fehler des Artikels möchte ich nicht eingehen, mir reicht es, den Fehler im Bild, in der Argumentation zu finden zu finden. Nur wie?
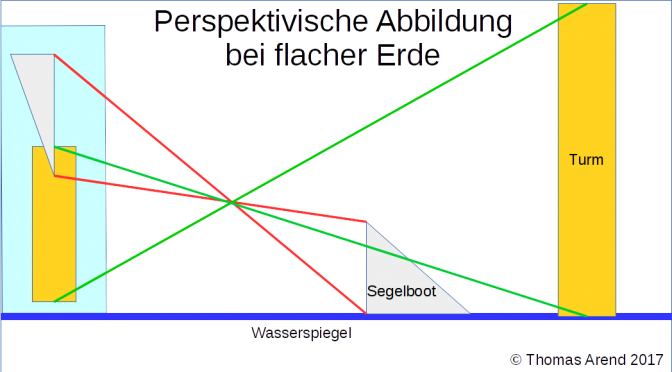
Die Segelschiffe am Horizont scheinen auf gleicher Höhe zu sein, wie das Ufer. Dies ist bei einer flachen Erde perspektivisch jedoch nicht möglich, wie folgende Skizze zeigt. Die fotografische Abbildung erfolgt kopfüber und Seiten verkehrt. Was weiter weg ist wird auch weiter oben im Bild abgebildet. Die Masthöhe eines kleinen Segelschiffes beträgt etwa zehn Meter. Ein Größenvergleich mit der Schlosskirche ergibt, dass die Segelschiffe zwischen fünf und sieben Kilometer vom Standort des Fotografen entfernt sein müssen.
Wenn also Segelschiffe auf der gleichen Höhe im Bild abgebildet werden wie das Ufer, dann müssen bei einer flachen Erde höher als das Ufer sein. Sie können also nicht im Wasser schwimmen. Einzige Lösung: Das Wasser hat einen Buckel oder Berg. Dann ist die Erde aber nicht flach sondern rund und – wenn der Rumpf zu sehen ist – schwimmen sie am Horizont.
Das Beweisfoto wurde angeblich von Konstanz bei einer Augeshöhe von vier Meter aufgenommen. Bis Friedrichshafen sind es etwa 18,4 km. Bei einer runden Erde müsste das Ufer erst ab zehn Meter Höhe zu sehen sein. Nach Aussage des Schreibers ist die Schlosskirche aber komplett zu sehen. Als „Beweis“ markiert er ein Fenster über der Eingangstür. Wie kann man dem widersprechen?
Nun, der helle Bereich unter dem Ufer ist Wasser und nicht wie behauptet Uferbauten. Weiße Uferbauten, die Licht so stark reflektieren könnten, gibt es dort nicht. Nach einigem Suchen fand ich ein Bild, das die Schlosskirche aus Richtung Immenstaad am Bodensee zeigt. Dies ist fast die gleichen Blickrichtung, nur ist Immenstaad nur etwa sieben bis acht Kilometer von Friedrichshafen entfernt. Aus vier Meter Augeshöhe ist das Ufer etwa auf Horizonthöhe und damit komplett sichtbar. Die perspektivische Verzerrung der Schlosskirche ist bei den großen Entfernungen vernachlässigbar. Also habe ich die beiden Bilder der Schlosskirche anhand markanter Linien auf den gleichen Maßstab skaliert und übereinander gelegt. Hier das Ergebnis:

Und hier als GIF:

Ganz offensichtlich ist ein Teil des Ufers von Konstanz aus nicht zu sehen.
Größe der Türme und des fehlenden Uferabschnitts habe ich in GIMP ausgemessen. Aufgrund der schlechten Auflösung des Beweisbildes liegt die Messgenauigkeit nur bei 30 cm pro Pixel. Etwas Dreisatz in LibreOffice Calc: Etwa neun bis zehn Meter des Ufers sind von Konstanz aus nicht sichtbar. Dies entspricht der Vorhersage des Modells einer runden Erde.
Auf die anderen mathematischen Künste des Artikeln gehe ich hier nicht ein.
Fazit: Auch am Bodensee lässt sich eine runde Erde beweisen. Es braucht dazu keinen Ozean.

Neueste Kommentare