Ist die Erde flach? (Teil 6)

[vgwort line=“92″ server=“vg05″ openid=“6af393ff7f0d4fc6a8b0dd1a6381abda“]

Nein, natürlich nicht!

In Teil 2 hatte ich schon über einen Artikel auf Euronia.com – Die Erde ist flach berichtet. Neben der Schlosskirche von Friedrichshafen und dem El Teide wird auch ein Bild des Meteorologen Alfons Puertas erwähnt. Das Bild zeigt die Serra de Tramuntana auf Mallorca von Barcelona aus. Angeblich beweist es, dass die Erde flach sein muss, denn die gesamte Serra de Tramuntana dürfte auf einer Kugelerde nicht zu sehen sein.

Die Argumentation des Autors ist falsch. Nur wo ist der Haken?

Auf die kleinen Fehler in der Berechnung möchte ich hier nicht eingehen. Ein Fehler ist, dass der Aufnahmestandort etwas höher ist, als angeben. Behauptet wird, dass
bei einer Entfernung von 200 km und einer Beobachterhöhe von 400 m die Berge unter Berücksichtigung der Refraktion bis zur Höhe 979 m nicht mehr sichtbar sind. Dadurch bleiben – nach der Berechnung des Autors – von der Gipfelhöhe der Serra de Tramuntana nur 466 m übrig. Der Autor glaubt den gesamten Gebirgszug deutlich zu erkennen, der auch wesentlich niedrigere Gipfel enthält. Hier liegt er leider falsch.

Das Observatori Fabra, Barcelona, Spanien ist mindestens 415 m hoch. Der Abstand der Serra de Tramuntana zum Observatorium beträgt etwa 187,5 km. Ohne die Refraktion zu berücksichtigen beträgt die nicht sichtbare Höhe ~ 1031m.

	Punk A		Punkt B
Radius RA	6.378.137,00	m	6.378.137,00	m
Augeshöhe Ah	415,00	m	1.031,98	m
Punkt bis Horizont	72.760,06	m	114739,94	m
Entfernung A-B	187.500,00	m	187.500,00	m

Aber die Frage ist nicht wie viel wirklich verdeckt wird. Als Gegenbeweis zur flachen Erde reicht es, wenn etwas durch den Horizont verdeckt wird.

Die Frage lautet daher:

Sehen wir wirklich den gesamten Gebirgszug?

Nein. Der Gebirgszug sinkt an einigen Stellen bis auf den Horizont ab. Wie kann das sein? Auf einer flachen Erde müsste die Insel dort geteilt sein. Es kann auch nicht die östlichen Inseln Menorca sein, denn es gibt mehrere solcher Einschnitte. Außerdem müsste man Menorca links in diesem oder ähnlichen Bildern sehen können.

Leider ist die Auflösung des Bildes mit 643 × 337 Pixel sehr dürftig. Zum Glück gibt es ähnliche Bilder, zum Beispiel von Marc Bret. Das Bild ist von deutlich besserer Qualität und das Observatori Fabra ist links im Bild zu erkennen. Das Bild wurde laut Marf Bret el Tibidabo, 512 m hoch, aufgenommen. Ohne Refraktion müssten Berge je nach genauem Abstand über 830 m bis 990 m zu erkennen sein. Der Fotograf hat dankenswerterweise die Berge, ihre Höhe und die Abstände im Bild markiert. Jetzt fehlen uns nur noch die Höhen über dem Horizont.

Hier eine Tabelle der Höhen der Berge und der Höhe über dem Horizont aus dem Bild von Marc Bret (Bild 1) und einem Bild von AlfonsPC – Observatori Fabravon.

Berg	Höhe in m	Entf. [km]	Bild 1	Bild 2	Meter / px	Meter / px
Puig Major	1436	189	46	52	31	28
Puig Massanella	1365	190	37	42	37	33
Puig Galileu	1182	189	26	28	45	42
Puig Tomir	1104	189	24	25	46	44
Puig Roig	1004	185	20	22	50	46
Puig Caragoler	922	185	16	16	58	58
Puig de lÓfre	1093	193	17	16	64	68
Puig Ternelles	839	184	11		76
Puig des Cà	876	189	11	6	80	146

Die Spalten Bild 1 und Bild 2 zeigen die Höhe des Berges über dem Horizont in Pixel im jeweiligen Bild. Aufgrund der Auflösung und Schärfe ist bei manchen Bergen die Messung schwierig. Je kleiner der Berg, desto größer der Fehler, den ein Pixel verursacht.

Wie man sieht, ist die Höhe eines Pixels stark abhängig von der Berghöhe. Je kleiner der Berg, desto größer muss ein Pixel. Die Streuung zwischen 31 m und 80 m bzw.  28 m und 146 m pro Pixel lässt sich nicht mit der Ungenauigkeit der Messung der Höhen und den leicht unterschiedlichen Abständen erklären. Wie die folgende Grafik anschaulich zeigt, besteht – von kleinen Ausreißern abgesehen – ein linearer Zusammenhang zwischen der Berghöhe in dem Abstand über dem Horizont. Nur geht eine nach links fortgesetzte gedachte Linie nicht durch den Nullpunkt (0,0).

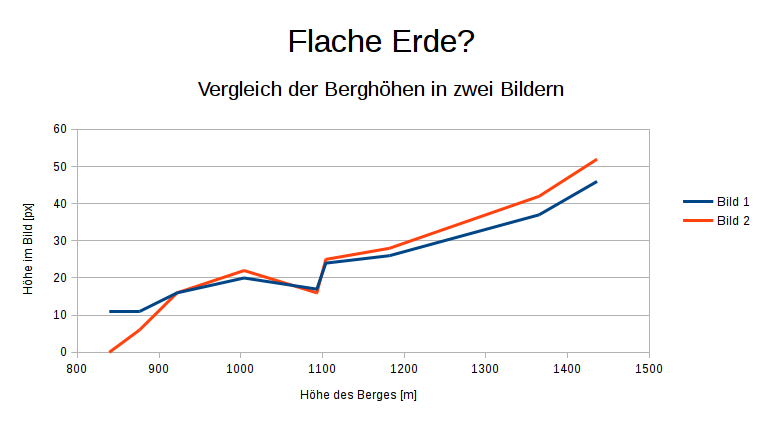
Dies ist nur damit zu erklären, der untere Teil des Gebirgszuges nicht zu sehen ist. Er kann nur vom Horizont verdeckt sein. D.h. die Erde muss sich hinter dem Horizont „absenken“ – sie muss gewölbt sein. Damit ist sie nicht flach.

Eine genaue Berechnung erspare ich mir. Hier geht es nur um die Frage, ob die Erde flach ist. Selbst ohne Berechnung zeigen die bis zum Horizont herab reichenden Lücken im Gebirgszug, dass Teile unter dem Horizont verschwinden und vom Meer verdeckt werden. Misst man die Höhen der Berge im Bild nach, dann stellt man fest, dass ein nicht unerheblicher Teil verdeckt sein muss.

Dies ist auf einer flachen Erde nicht möglich.

Fazit

Auch diese Bilder von Mallorca zeigen: Die Erde ist nicht flach.

Übrigens: Berichte, dass die Berge auch von der Küste zu sehen sind, gibt es nicht und Bilder vom etwa gleich weit entfernten Menorca im Osten gibt es auch nicht. Der höchste „Gipfel“ Monte Toro ist nämlich nur 357 m hoch. Aber ein Gläubiger der flachen Erde wird sich dadurch nicht irritieren lassen.

Weitere Bilder

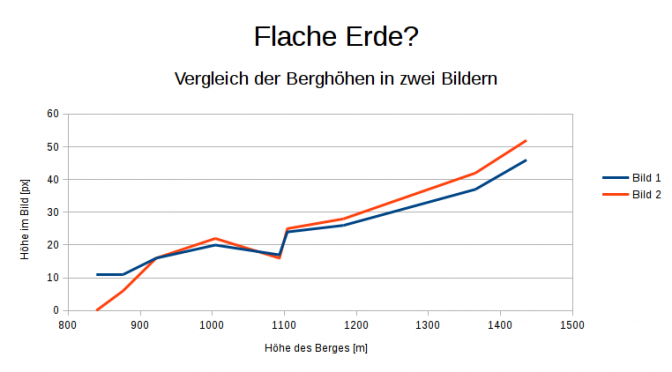
Auf Flickr finden sich weitere Bilder unter AlfonsPC – Observatori Fabra mit besserer Auflösung.- aufgenommen aus einer Höhe von ~415 m. Vergleicht man eines der dieser Bilder mit dem Bild von Marc Bret, aufgenommen auf ~ 512 m, dann stellt man fest, dass der Puig Ternelles unter dem Horizont verschwunden ist. Wie soll dies auf einer flachen Erde gehen?