Ist die Erde flach? (Teil 2)

[vgwort line=“90″ server=“vg05″ openid=“5675208fa34b4c159a0a4ca8d68a622b“]
Nein, natürlich nicht! Wie ich bereits vorherigen Artikel zu Thema beschrieben habe, „beweisen“ Anhänger der Theorie der flache Erde gerne, dass die Erde flach ist. Da sie aber mehr oder weniger eine Kugel ist, müssen diese „Beweise“ falsch sein. Aber wo liegt der oder liegen die Fehler in den einzelnen Beweisen. Neben der Schlosskirche von Friedrichshafen wird ein Bild des El Teide, angeblich von El Cotillo aus aufgenommen, in dem Artikel Euronia.com – Die Erde ist flach als Beweis angeführt. Dieses Bild ist von Jo Hammer auf Facebook zu bewundern. Statt den Fotografen zu fragen, wo von wo er das Bild aufgenommen hat, wird auf die Aussage einer Bewohnerin zurückgegriffen. Aber dazu zum Schluss mehr.

Obwohl der El Teide gut 260 km von El Cotillo entfernt liegt, ist er vor der untergehenden Sonne zu sehen. Da die Häuser in El Cotillo nur drei Stockwerke haben, müsste der Berg über 4.900 Meter hoch sein, damit er über den Horizont hinausragt. Auch wenn vom Leuchtturm (34 m hoch) fotografiert wurde, reicht die Augeshöhe nicht um die Spitzen des El Teide zu sehen.

Ein Beweis für die flach Erde? Mitnichten! Dank der untergehenden Sonne können wir dies sogar anhand des Bildes beweisen. Der El Teide ist nämlich nicht vollständig zu sehen.

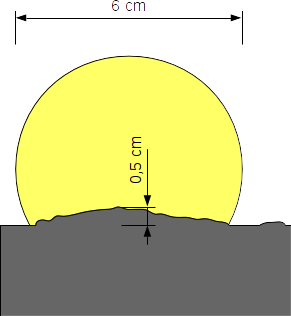
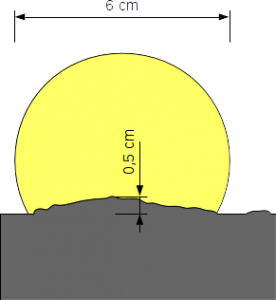
Die scheinbare Größe der Sonne am Firmament ist ungefähr 30 Bogenminuten oder 0,5°. Die scheinbare Höhe der Berge über dem Horizont beträgt nur ungefähr 0,05°; etwa ein Zehntel der Größe der Sonne, wie die folgende Skizze zeigt. Dazu habe ich das Bild in LibreOffie Draw eingebetten und die wichtigsten Element eingezeichnet und das Bild anschließend wieder entfernt um Urheberrechtsfragen zu umgehen.

Mit ein wenig Dreisatz können wir die Höhe der Berge in Meter über dem Horizont berechnen. (Für diese Rechnung habe ich die Pixelmaße mit GIMP dem Original entnommen.)

	Maß	Einheit	Formel
Höhe Sonne (Hs)	235,00	px
Höhe Berge (Hb)	22,00	px
Winkel Sonne (αs)	0,50	°
Winkel Berge (αb)	0,05	°	Hb/Hs*αs
Abstand Berge	261690	m
Höhe Berge	214	m	2*π*r*αb/360

Wie man sieht, ragen die Berge auf dem Bild nur etwa 214 Meter über den Horizont hinaus. Der El Teide ist aber 3.718 Meter hoch. Über 3.504 Meter sind gar nicht sichtbar, sondern verdeckt. Nur das Wasser des Ozean kann diesen Teil verdecken. Dies ist auf einer flachen Erde nicht möglich. Dass heißt, die Erde muss dort gewölbt sein oder vereinfacht rund sein. Auch kann das Bild nicht von El Cotillo aufgenommen worden sein. Um dieses Bild auf einer runden Erde aufzunehmen muss der Fotograf auf einen Berg gestiegen sein, der etwa 200 Meter hoch ist, wie folgende Rechnung zeigt. Ab einer Höhe von etwa 3.500 Meter sind die Berge sichtbar. Dies ist die Augeshöhe des Punktes A. Damit dies im Abstand von etwa 260 km sichtbar ist, muss man im Punkt B auf eine Augeshöhe von ~198 Meter steigen.

	Punk A		Punkt B
Radius RA	6.378.137,00
Augeshöhe Ah	3.504,21	m	197,83	m
Horizont	211.454,32	m	50.235,68	m

Schauen wir uns in der Umgebung von El Cotillo um, dann finden wir bei OpenStreetmap den Mt. da la Costilla, einen Aussichtspunkt, der mit 192 Meter die benötigte Höhe hat. Da die Sonne im Bild nur etwa 235 px breit ist, und die Berge 22 Pixel hoch sind, beträgt die Messgenauigkeit etwa 10 Meter. Im Artikel wird auch geschrieben, dass das Foto von El Costillo aufgenommen wurde. Vielleicht liegt hier nur ein Missverständnis aufgrund der verschiedenen Schreibweisen vor?

Da hilft nachfragen beim Fotografen. Mal sehen, ob ich eine Antwort bekomme.

Es gibt auch andere Bilder, da ist der El Teide von Fuerteventura deutlich besser zu sehen. Aber es ist nicht die gesamte Insel zu sehen. Leider auch keine Sonne als Maßstab.

Fazit: Unabhängig von der Antwort, auch dieses Bild beweist, dass die Erde nicht flach ist, sonder eine Kugel ist – mehr oder weniger.