Curvature of the Earth: Eight inches per mile squared?

Flat-Earthists ( see: Zetetic astronomy. Earth not a globe! an experimental inquiry into the true … from Samuel Birley Rowbotham) always claim that the curvature of the Earth is eight inches per mile squared. Sometimes Flat Earthers are taught that this is not the correct formula and that a sphere is not a parabola. That’s basically true, but where does this rule of thumb come from?

The distance d from the height of the eye h to the horizon can be calculated on a sphere using the formula of Pythagoras (R + h)² = R² + d², where R is the radius of the sphere. From this formula, a rule of thumb for small heights can be derived as follows.

( R + h ) ^ 2 = R ^ 2 + d ^ 2 R ^ 2 +2 * R * h + h ^ 2 = R ^ 2 + d ^ 2 2 * R * h + h ^ 2= d ^ 2 with R >> h => 2 * R * h approx d ^ 2 h approx { d ^ 2 } over { 2 * R } with R approx 6371000 m => h approx 7.8481 * 10 ^ - 8 [m^-2] * d ^ 2 or : 7.8481 cm / km ^ 2
Derivation of the rule of thumb

In the metric system we get about 8 cm per distance kilometer squared. That equates to 8 inches per mile squared.

The following diagram shows the difference between the approximation formula and the exact value and the distance from the base of the observation to the horizon.

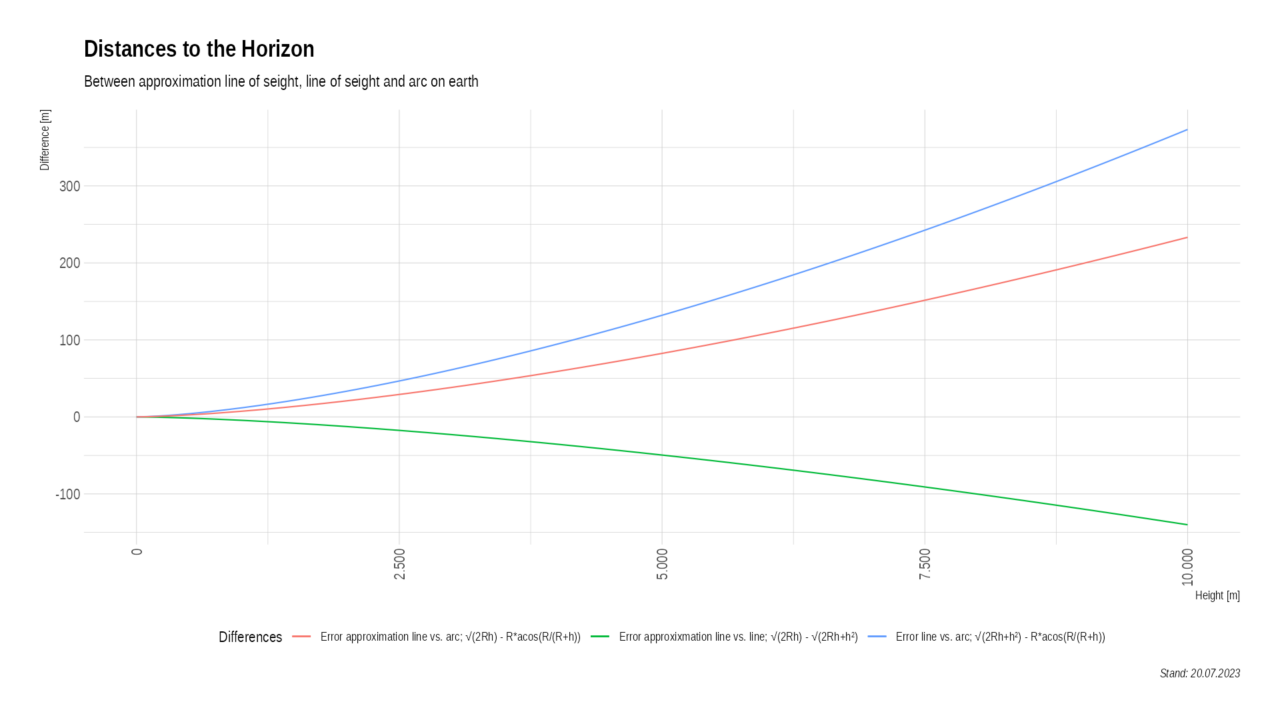
The diagram shows the differences in the calculations of the distance to the horizon. The observation height is entered on the x-axis and the difference between three different calculation methods is entered on the y-axis 1 approximation formula 2 exact calculation with Pythagoras 3 Calculation of the distance from the base point to the arc. The approximation formula underestimates the distance to the horizon. The distance on the arc at level 0, the map distance, is overestimated. At 10,000 m altitude, the error between the approximation and the exact formula is less than -150 m. To the distance on the circular arc, the error is less than + 350 m. This is practically negligible at 350 km to the horizon.

The distance to the horizon at an altitude of 10,000 m is 357099.4 m. The difference of -140 m to the result of the approximation formula is negligible at -0.04%. Conversely, to determine eye level from a distance, the formula can also be used. When rounded up to 8 cm, the relative error is less than 2%.

Conclusion

For practical applications, the rule of thumb is sufficiently accurate. Especially when it comes to determining the invisible height behind the horizon in images with poor resolution.

Schlagwörter