How to prove that the earth is not flat without leaving your home.
A step by step method
Follow the following steps
- Open Google Maps
- Locate your house or garden
- Pick two positions (A and B) in line of sight. One should be east or west of the other. You can also pick two points that you know the distance from.
- Note the latitude/longitude (A.lat, A.lon, B.lat and B.lon in °) of the positions (right click) and measure the distance with Google.
- If you don’t know the distance, you should measure the actual distance now (with a laser pointer).
Now we perform the following calculations:
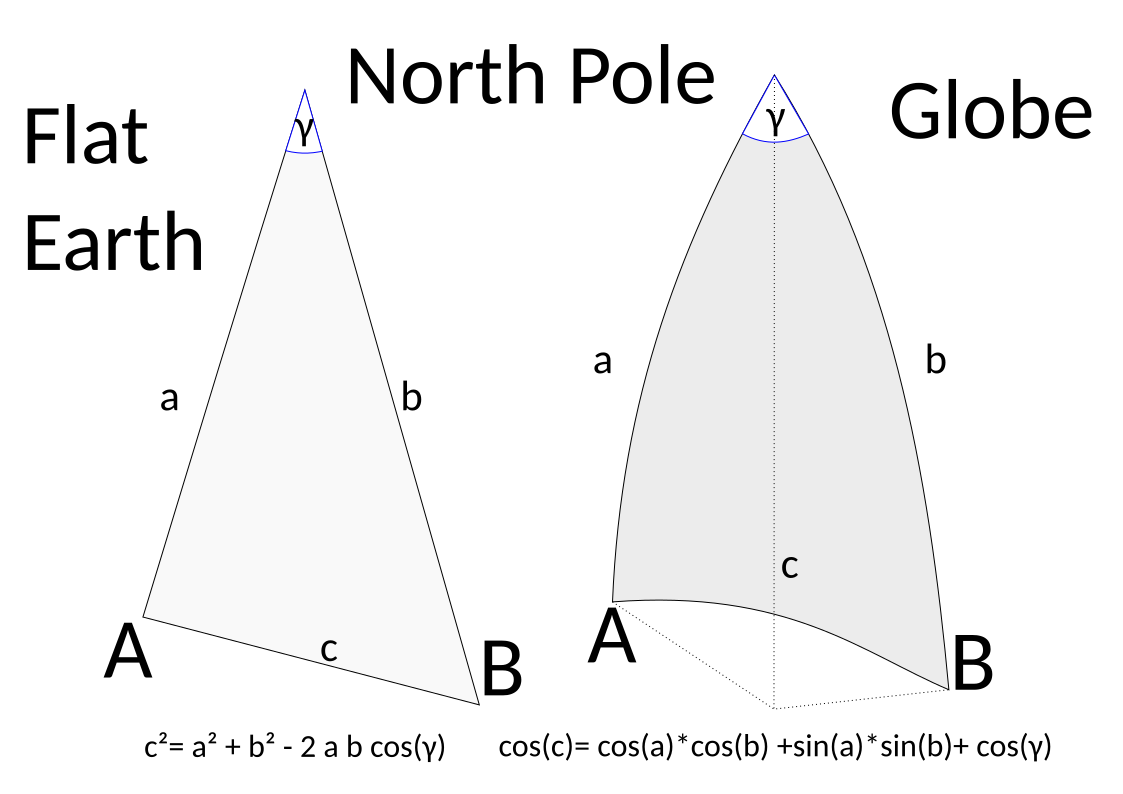
- Build a triangle between the North Pole and the two positions.
- The distances (a and b) of the points to the North Pole should be equal on a flat earth and a globe.
- The angle between the points also stays the same.
- Calculate a = (90 – A.lat) / 180 * pi, b = (90 – B.lat) / 180 * pi
- On a flat earth, the distance c would be R * sqrt( a² + b² – 2 * a * b * cos(γ) ) with R the radius of the globe.
I.a.w. the law of cosine for eucledian trigonometry - On a globe the distance would be c = R * acos( cos(a)* cos(b) + sin(a) * sin(b) * cos(γ) )
I.a.w. the law of side cosine of spherical trigonometry.
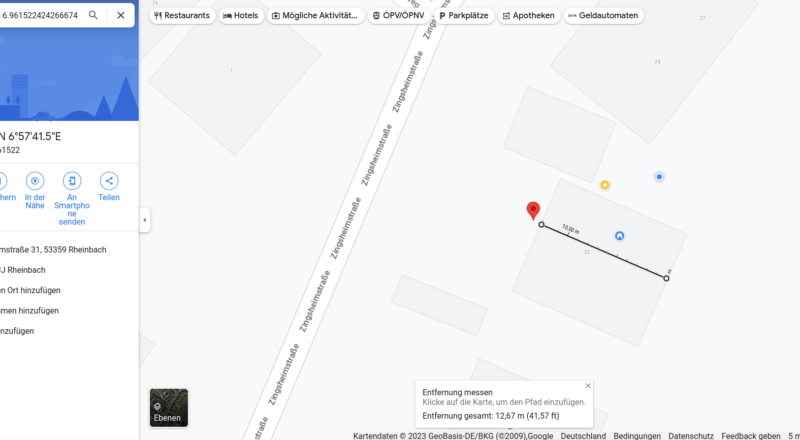
In my case I got from Google for A = ( lat = 50.62091719914353, lon = 6.961698755042375)
and
B = ( lat = 50.62096229478388, lon = 6.9615317875405385). The distance is 12,67 m.
The actual value is approximately 12 m with roof. You can’t pick the positions of two points on Google exactly and thus measure the distance very well. That’s why I don’t care about small differences.
On a flat earth the distance would be 13.7 m, on a globe it would be 12.8 m. That’s a difference of 90 cm.
Conclusion:
The result is much closer to reality, if I assume that the earth is not flat.
R-Script
R-Script to calculate the distance between two points on a globe and on an flat earth
#!/usr/bin/env Rscript
# Radius of Earth
R = 6371000.785 # meter
# Points
# 50.62091719914353, 6.961698755042375
# 50.62096229478388, 6.9615317875405385
points = list (
A = list (
lat = 50.62091719914353
, long = 6.961698755042375
) ,
B = list (
lat = 50.62096229478388
, long = 6.9615317875405385
)
)
Gamma = ( points$A$long - points$B$long ) / 180 * pi
A = ( 90 - points$A$lat ) / 180 * pi
B = ( 90 - points$B$lat ) / 180 * pi
cat ('Distance on a\n')
C = acos( cos(A)* cos(B) + sin(A) * sin(B) * cos(Gamma))
cat ( "globe:\t" , C * R , 'meter\n')
C = sqrt( A^2 + B^2 - 2 * A * B * cos(Gamma) )
cat ( 'flat earth:\t', C * R, 'meter\n' )
Output
Distance on a
globe: 12.80184 meter
flat earth: 13.71018 meterIf you are not satisfied
Have a look at this map.
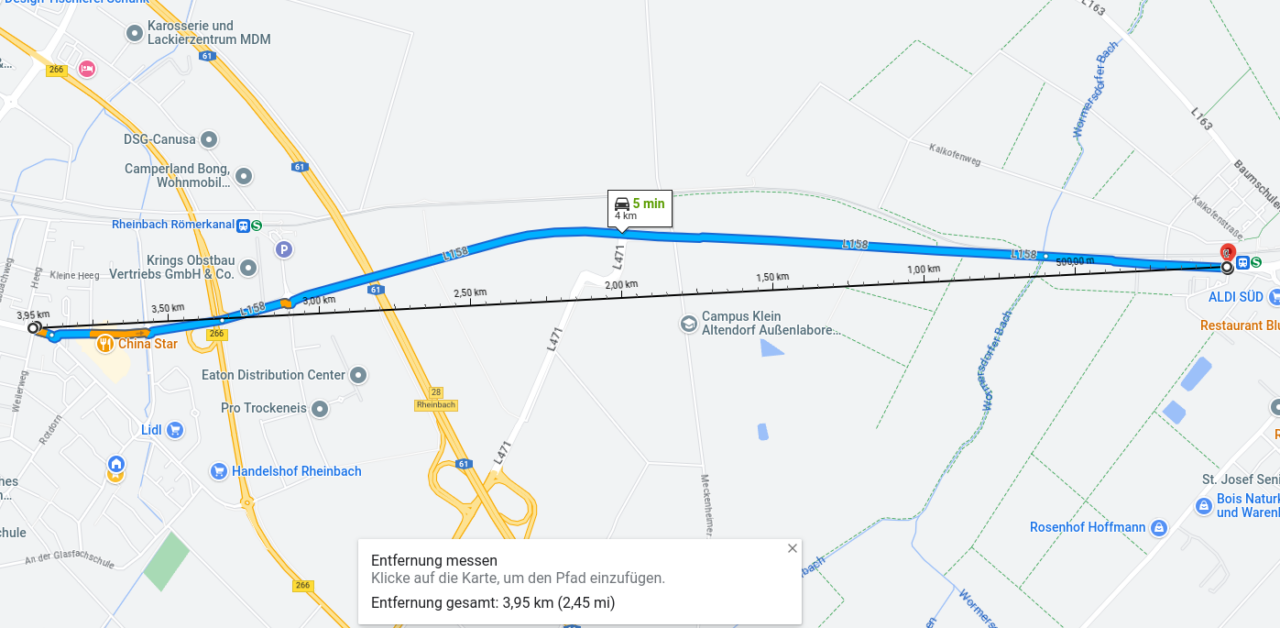
Look for a distance you can drive by car. On a flat earth the distance would be 8.3 % higher than on a globe.
Distance on a globe: 3935.326 meter flat earth: 4263.011 meter Flat Earth / Globe 1.083267
Still not satisfied?
Then we go to Mill Road in Cape Town (lat=-33.92475259959898, lon=18.652255231296) and zoom in on the map as much as possible. There is a truck on the road. We measure the length and position of the beginning and end of the vehicle with Google maps.

According to Google Maps, the vehicle is about 18 m long. That is a plausible length for a truck.
It starts and ends at the geographic positions
A = -33.924745346886986, 18.652164072490983
B = -33.924758144201505, 18.652357862081466
Calculating the length between the geographic points we get following values:
Distance on a globe: 17.937 meter flat earth: 46.62861 meter Flat Earth / Globe 2.599577
The result of about 47 m instead of 18 m cannot be explained by measurement errors. Calculations on an Euclidean level lead to values that do not correspond to reality. Flat earthers should be able to explain these differences and calculate the correct value based on a flat earth.
However, the solution is simple: If the earth is a globe, then reality and calculated result match.

Neueste Kommentare