[vgwort server=vg02 openid=“a6ce43f660b747a5bb3624623fc2cc98″ line=1]
Um die Antwort vorwegzunehmen: Ja!
Das RKI veröffentlicht die wöchentlichen Testungen und die positiven Ergebnisse zu SARS-CoV-2, COVID-19 oder Corona seit der 10. Kalenderwoche 2020. Die Zahlen habe ich in der unten abgebildete Tabelle zusammengetragen und um die von mir geschätzte Prävalenz (der Anteil der wirklich Infizierten unter den Getesteten) erweitert.
Nur steigen die Zahl der Testungen und die Zahl der positiv Testergebnisse. Da könnte das Eine das Andere bedingen, ohne dass sich die Grundsitiation in der Bevölkerung geändert hat. Einige bezweifeln daher, dass wir wieder steigende Zahlen haben. Manche behaupten, die positiven Test stammen nur aus dem Testfehler und es gäbe keine Infizierten (mehr).
| KW | Testungen | Positiv getestet | Positiv [%] | Prävalenz | True positive | True negative | False positive | False negative | PPP | Infiziert (geschätzt) |
| 10 | 124.716 | 3.892 | 3,12 % | 2,84 % | 3.536 | 121.056 | 364 | 4 | 90,68 % | 3.539 |
| 11 | 127.457 | 7.582 | 5,95 % | 5,67 % | 7.221 | 119.868 | 361 | 7 | 95,24 % | 7.229 |
| 12 | 348.619 | 23.820 | 6,83 % | 6,56 % | 22.843 | 324.776 | 977 | 23 | 95,90 % | 22.866 |
| 13 | 361.515 | 31.414 | 8,69 % | 8,42 % | 30.421 | 330.071 | 993 | 30 | 96,84 % | 30.451 |
| 14 | 408.348 | 36.885 | 9,03 % | 8,77 % | 35.767 | 371.427 | 1.118 | 36 | 96,97 % | 35.803 |
| 15 | 380.197 | 30.791 | 8,10 % | 7,83 % | 29.740 | 349.376 | 1.051 | 30 | 96,59 % | 29.769 |
| 16 | 331.902 | 22.082 | 6,65 % | 6,38 % | 21.150 | 309.799 | 932 | 21 | 95,78 % | 21.171 |
| 17 | 363.890 | 18.083 | 4,97 % | 4,69 % | 17.043 | 345.790 | 1.040 | 17 | 94,25 % | 17.060 |
| 18 | 326.788 | 12.608 | 3,86 % | 3,57 % | 11.663 | 314.168 | 945 | 12 | 92,50 % | 11.674 |
| 19 | 403.875 | 10.755 | 2,66 % | 2,37 % | 9.572 | 393.110 | 1.183 | 10 | 89,00 % | 9.582 |
| 20 | 432.666 | 7.233 | 1,67 % | 1,38 % | 5.953 | 425.427 | 1.280 | 6 | 82,30 % | 5.959 |
| 21 | 353.467 | 5.218 | 1,48 % | 1,18 % | 4.170 | 348.245 | 1.048 | 4 | 79,92 % | 4.174 |
| 22 | 405.269 | 4.310 | 1,06 % | 0,77 % | 3.104 | 400.956 | 1.206 | 3 | 72,01 % | 3.107 |
| 23 | 340.986 | 3.208 | 0,94 % | 0,64 % | 2.192 | 337.776 | 1.016 | 2 | 68,32 % | 2.194 |
| 24 | 326.645 | 2.816 | 0,86 % | 0,56 % | 1.842 | 323.827 | 974 | 2 | 65,40 % | 1.843 |
| 25 | 387.249 | 5.307 | 1,37 % | 1,07 % | 4.158 | 381.938 | 1.149 | 4 | 78,34 % | 4.162 |
| 26 | 466.743 | 3.673 | 0,79 % | 0,49 % | 2.280 | 463.068 | 1.393 | 2 | 62,06 % | 2.282 |
| 27 | 505.518 | 3.080 | 0,61 % | 0,31 % | 1.568 | 502.436 | 1.512 | 2 | 50,91 % | 1.570 |
| 28 | 509.398 | 2.989 | 0,59 % | 0,29 % | 1.465 | 506.408 | 1.524 | 1 | 49,02 % | 1.467 |
| 29 | 537.334 | 3.480 | 0,65 % | 0,35 % | 1.874 | 533.852 | 1.606 | 2 | 53,84 % | 1.876 |
| 30 | 563.553 | 4.364 | 0,77 % | 0,48 % | 2.681 | 559.186 | 1.683 | 3 | 61,44 % | 2.684 |
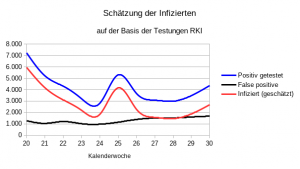
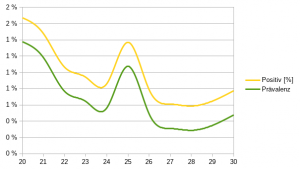
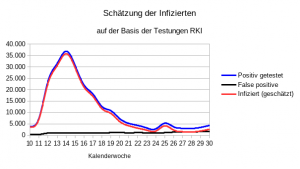
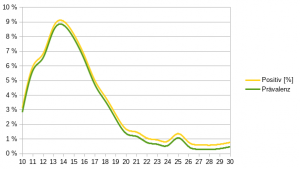
Schauen wir uns die Tabelle an, dann sehen wir, dass die Testungen von 120.716 auf 563.553 gestiegen ist und dass das der Anteil der positiven Testergebnisse von 3,12% über 9,03% auf 0,77% gesunken ist. In der Anfangszeit war die Testkapazität zu gering. Über eine Vorauswahl wurde die Vortestwahrscheinlichkeit erhöht. Dies ist auch aufgrund der Testfehler sinnvoll. Die Getesteten der Anfangszeit waren nicht repräsentativ für die gesamte Bevölkerung. Durch Kontaktverfolgung wurde die Vortestwahrscheinlichkeit in die Höhe erhöht.
Mit der Ausweitung des Testkapazitäten wurden die Voraussetzungen für einen Test reduziert. In Folge sollte die Vortestwahrscheinlichkeit sinken, was mit einer Ausnahme von der 14 bis zur 28 Kalenderwoche der Fall war. Dabei sank in der Zeit sogar die Zahl der Testungen. Die 25. Kalenerwoche könnte als Tönnieswoche bezeichnet werden.
Nach dem Tief in der 27. und 28. Kalenderwoche kehrte sich der Trend um. Ob er anhalten wird, ist die spannende Frage.
Wie komme ich nur zur Schätzung der Prävalenz?
Ein Test hat zwei Ausgänge, er ist positiv oder negativ. Jeder Getestet hat einen von zwei Zuständen. Er ist entweder infiziert oder nicht infiziert (gesund).
Nun können vier Fälle eintreten:
- TP: Probant infiziert, Test erkennt es = richtig positiv / true positive (bedingte Wahrscheinlichkeit tp)
- FN: Probant infiziert, Test erkennt es nicht = falsch negativ / false negative (bedingte Wahrscheinlichkeit fn)
- TN: Probat gesund, Test erkennt es = richtig negativ / true negativ (bedingte Wahrscheinlichkeit tn)
- FP: Probant gesund, Test erkennt ihn als infiziert = falsch positiv / false positive (bedingte Wahrscheinlichkeit fp)
Die Fälle 2 und 4 sind Fehler des Testes. In Ringtestversuchen wird die Wahrscheinlichkeit für diese Fehler bestimmt. Gute Teste für SARS-CoV-2 / COVID-19 haben Sensitivität nahe 100%, d.h. ein Infizierter wird mit dieser Wahrscheinlichkeit als Infiziert erkannt (Testausgang: true positive). Die Spezifität liegt zwischen 98,6 und 99.8%, d.h. ein Gesunder wird mit dieser Wahrscheinlichkeit als gesund erkannt.
Die Sensitivität ist gleich (1 -fn) und die Spezifität ist (1-fp). (tp + fn) = 1 und (tn+fp) = 1. Für die obige Tabelle habe ich eine Sensitivität von 99,9% und eine Spezifität von 99,7% angenommen.
Wenn unter T Getesteten P infiziert sind, dann beträgt die Prävalenz p (Wahrscheinlichkeit eines Getestet infiziert zu sein) P/T. Die Prävalenz p ist ein Schätzwert, wie viele Infizierte in der Gesamtbevölkerung sind.
Richtig ist nun, dass wenn sehr wenige erkrankt sind, ein Test sehr viele Gesunde als krank meldet. So richtig gut funktioniert ein Test nur, wenn Infizierte und Gesunde sich die Waage halten.
Nun stehen TP, FN, TN, FP, Sensitivität und Spezifität in folgenden Beziehungen:
TP = T * p * ( 1 - fn ) FN = T * p * fn TN = T * ( 1 - p ) * ( 1 - fp ) FP = T * ( 1 - p ) * fp
Die Zahl der positiv getesteten ergibt sich aus der richtig positiv und falsch positiv getesteten (TP und FP). Nun ergibt sich:
P = TP + FP = T * p * ( 1 - fn ) + T * ( 1 - p ) * fp
oder
p = ( P -fp*T ) / ( T * ( 1 - fn ) - fp * T )
Mit diesem Wissen – oder diesen Annahmen – können wir nun die Testergebnisse um die (geschätzten) Fehler bereinigen.
Ein Bild sagt mehr als 1.000 Worte, …
Woher habe ich die Spezifität 99,7%
Die Hersteller halten sich mit der Spezifität und der Sensitivität leider etwas stark bedeckt. Es gibt unterschiedlich angaben und in der Anfangszeit war die Spezifität eher schlecht. Die Angaben nahezu 100% bei der Sensitivität habe ich mit 99,9% angenommen. Für die Spezifität habe ich verschieden Berichte ausgewertet und kam auf einen besten Wert von 99,8%. Ich habe mich dann für 99,7 entschieden.
Die Teste sind aber viel schlechter
Nein. Und es würde nichts am Ergebnis ändern. Schauen wir und die 28. Kalenderwoche an. Wenn es nicht einen Erkrankten gab und alle positiven Teste auf falschen Ergebnissen beruhen, war die Spezifität 99,41%. Mit dieser Spezifität ergibt sich folgende Tabelle. Auch in diesem Fall kehrt sich der Trend ab der 28. Kalenderwoche um.
| KW | Testungen | Positiv getestet | Positiv |
Prävalenz |
True positive | True negative | False positive | False negative | PPP | Infiziert (geschätzt) |
| 25 | 387.249 | 5.307 | 1,37 % | 0,79 % | 3.053 | 381.939 | 2.254 | 3 | 57,52 % | 3.056 |
| 26 | 466.743 | 3.673 | 0,79 % | 0,20 % | 940 | 463.069 | 2.733 | 1 | 25,59 % | 941 |
| 27 | 505.518 | 3.080 | 0,61 % | 0,02 % | 114 | 502.438 | 2.966 | 0 | 3,72 % | 115 |
| 28 | 509.398 | 2.989 | 0,59 % | 0,00 % | 0 | 506.409 | 2.989 | 0 | 0,00 % | 0 |
| 29 | 537.334 | 3.480 | 0,65 % | 0,06 % | 329 | 533.854 | 3.151 | 0 | 9,45 % | 329 |
| 30 | 563.553 | 4.364 | 0,77 % | 0,19 % | 1.063 | 559.188 | 3.301 | 1 | 24,37 % | 1.065 |
Wie man sieht, steigt auch in diesem Fall die Prävalenz, d.h. der Anteil der wirklich Erkrankten.
Was ist PPP
Sie positive Vorhersagekraft, Positive Predictive Power (PPP), ist die Wahrscheinlichkeit, mit der ein positiv Getesteter tatsächlich infiziert ist. In den ersten Kalenderwochen war diese noch recht hoch. Inzwischen sind aber nur wenige Infiziert. D.h. ein Großteil der positiv Getesteten stammt von den falsch getesteten Nicht-Infizierten.
Ist das schlimm? Nein, wenn jeder positiv Getestete einen zweiten Test macht, um den ersten zu bestätigen. Dazu sollte natürlich ein anderer Test gewählt werden, um einen reproduzierenden Fehler des verwendeten Tests auszuschließen. Aber das führt jetzt zu weit ab vonm Weg.
Zum Schluss ein Beispiel für eine Doppeltestung der gesamten Bevölkerung bei positivem ersten Test. Die positive Vorhersagekraft wird durch dieses Verfahren von 77,1% auf 99,6% erhöht. Aber: Bei einem Massentest übersehen wir bei einer Sensitivität von 99,9% in 1.663 infizierte, die dafür sorgen, dass es nicht aufhören wird.
| Anzahl Tests | Prävalenz | Testfehler | Infizierte [+] nicht Infizierte [-] |
Test-Ergebnisse | Test-Ergebnisse | Vorhersagewert | ||||
| Test 1 | ||||||||||
| 83.200.000 | 1,00% | Sensivität | 99,90% | + | 832.000 | 1.078.272 | True |
831.168 | 77,083% | |
| False |
832 | |||||||||
| Spezifität | 99,70% | – | 82.368.000 | 82.121.728 | True |
82.120.896 | 99,999% | |||
| False |
247.104 | |||||||||
| Test 2 | ||||||||||
| 1.078.272 | 77,08% | Sensivität | 99,90% | + | 831.168 | 831.078 | True |
830.337 | 99,911% | |
| False |
831 | |||||||||
| Spezifität | 99,70% | – | 247.104 | 247.194 | True |
246.363 | 99,664% | |||
| False |
741 | |||||||||
Zum Schluss
Hier noch die LibreOffice Tabellen um es prüfen zu können.

Neueste Kommentare