Kurzfassung
In diesem Beitrag beschreibe ich zwei Ansätze die Schutzwirkung von Impfungen auf den Daten des RKI für Fallzahlen und Impfungen abzuschätzen. Aufgrund der nicht sehr detaillierten Daten sind die Schätzungen eher grob und dienen mir nur andere Aussagen auf Plausibilität zu prüfen.
Der erste Ansatz nutzt die R-Zahl. Wenn die Impfung vor Infektion schützt müsste die R-Zahl entsprechend des Schutzes sinken. Eine Ungeimpfte und eine geimpfte Kontrollgruppe müssten daher Unterschiede in der R-Zahl aufweisen. Im Monat August ergibt sich für die Altersgruppen ein Schutz von
- A60-79: 11,5% [CI95%: 1,2% – 20,9%]
- A80+: 9,2% [CI95%: -1,3% – 18,7%]
Das Ergebnis entspricht nicht ganz anderen Ergebnissen, liegt aber noch am unteren Rand der Vertrauensintervalle.
Der zweite Ansatz geht über die Case Fatality Rate (CFR).
Aus der CFR zum 01.08.2021 über die Zeit von sechs Wochen ergibt sich ein Schutz vor Infektion, wenn die Impfung zu 100% vor Tod schützt, von
- A60-A79: 46,93% [CI 95%: 18,61% – 64,73%]
- A80+: 58,88% [CI 95%: 37,37% – 73,10%]
Umgekehrt gilt: Schützt die Impfung nicht vor Infektion, schützt sie vor Tod:
- A60-A79: 79,04% [CU 95%: 64,50% – 93,59%]
- A80+: 69,96% [CU 95%: 55,10% – 84,83%]
Diese Ergebnisse will ich im folgenden erläutern.
Fragestellung
Kann man die Wirksamkeit der Impfstoffe aus den vom RKI bereitgestellten Daten ableiten?
Unter https://github.com/robert-koch-institut stellt das RKI Daten zu den Fallzahlen und den Impfungen bereit. Davon werden 2 Dateien benötigt:
Diese Dateien importiere ich in eine MariaDB um die Daten mit RScript abzufragen und auszuwerten. Mit den Details wollen wir uns hier nicht aufhalten.
Werfen wir einen Blick auf die Fallzahlen nach Altersgruppe.
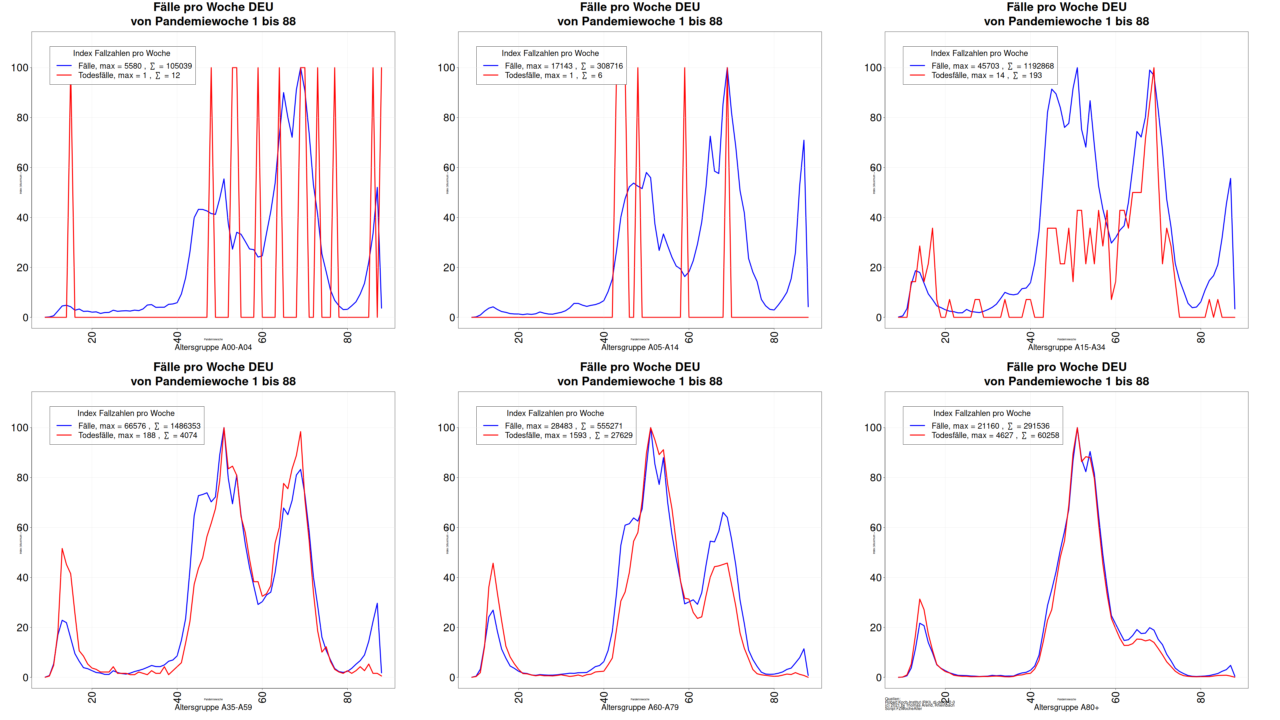
In der dritten Welle stagnierten die Fallzahlen der Altersgruppe A80+, während in allen anderen Altersgruppen die Fallzahlen stiegen. Auch die Altersgruppe A60-A79 stieg nicht so stark an und die Todesfallzahlen liegen deutlich unter den zu erwartenden Fallzahlen. Dies können wir als Ansatz zur Berechnung des Impfschutzes nutzen.
Leider sind die Daten des RKI nicht sonderlich gut aufeinander abgestimmt. Die Alterseinteilung ist zu grob. Insbesondere gibt es bei den Impfungen nur drei Altersgruppe. Die Altersgruppe A60+ teilt sich in den Fallzahlen auf zwei Altersgruppen A60-A79 und A80+ auf. Zwar ließen sich die Altersgruppen zusammen fassen, aber wirklich etwas gewonnen ist damit nicht. Also nehme ich in Kauf, dass zumindest im Anfang der Impfungen die Impfquote der A80+ unterschätzt und die Impfquote der A60-A79 überschätzt werden. Gegen Ende dürften sich beide der Sättigung bei 85% genähert haben. Die Berechnungen lassen sich täglich fortführen und werden sicher dank steigender Fallzahlen in der vierten Welle statistisch stabiler.
Frage 1: Schützen die Impfstoffe vor Infektion
Um zu bestimmen, ob die Impfungen vor Infektion schützen, gehen wir von einem SIR-Modell, einer geimpften und einer ungeimpften Gruppe und folgender Überlegung aus: Genesene und Infizierte sind zu 100% geschützt, was nicht Stand des Wissens ist. Quelle
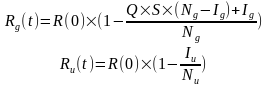
dabei ist
- u, g = ungeimpft, geimpft
- N = Größe der Gruppe
- I = Anzahl der Infizierten in der Gruppe
- Q = die Impfquote
- S = Schutz vor Infektion
Aufgrund der oberen Formel ist bei einer Impfquote von 80% und einem Schutz von 100% bei 5% Infizierten für Geimpfte eine R-Zahl etwa einem Sechstel der Ungeimpften erwarten. Das ist aber derzeit nicht der Fall.
Aus den Fallzahlen lässt sich R(t) bestimmen, die Impfquote erhalten wir aus der Tabelle des RKI und die Größe der Bevölkerungsgruppe vom Bundesamt für Statistik (Stichtag 2019-12-31).
Als Ungeimpfte nehmen wir die Altersgruppe A05-A14 und als Geimpfte die Altersgruppe A60-A79 und A80+.
Leider denken sich die Altersgruppen der Fallzahlen (0-4, 5-14, 15-34, 35-59, 60-79 und 80+) nicht mit den Altersgruppen der Impfungen (12-17, 18-59 und 60+). Für A60-79 und A80+ könne wir daher nur die Impfquote der Altersgruppe A60+ zugrunde legen. Wir könnten natürlich A60-79 und 80+ zusammenlegen, das hilft aber nur bedingt, den es wurde von alt nach jung geimpft.
Das RKI müsste hier an einheitlichen Berichtsstandards arbeiten.
Da wir zwei Gleichungen haben, können wir den R(0) eliminieren und es verbleibt als zu berechnender Wert der Schutz S. Nach einigen Umformungen ergibt sich für den Schutz:
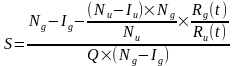
Jetzt geht es ans Abfragen und Rechnen.
Die R-Zahl ermitteln wir mit einer Regressionsanalyse. Wir nehmen an, dass die R-Zahl innerhalb eines Zeitintervalls relativ konstant ist.
Die obige Formel besagt zwar, genau das Gegenteil, aber in einem kleinen Zeitraum bis zu sechs Wochen verschwindet diese Ungenauigkeit in der Volatilität der Fallzahlen. Besser als +/- 5% lässt sich R(t) kaum bestimmen. Wenn N sehr groß ist und die Differenz der Infizierten zwischen Beginn und Ende klein, sind die Verhältnisse (N-I(t))/N nahezu konstant. Bei 83.Mio Einwohnern, 4 Mio Infizierten beträgt der Einfluss von 100.000 Infizierten nur 4% auf die Infizierten. Für die Infizierten nehmen wir daher die Zahl der Infizierten am Ende des Intervalls. Vielleicht könnte man etwas Genauigkeit gewinnen, wenn der Mittelpunkt oder der Mittelwert genommen wird. Durch die Wahl des oberen Wertes für die Infizierten unterschätzen wir den Schutz etwas.
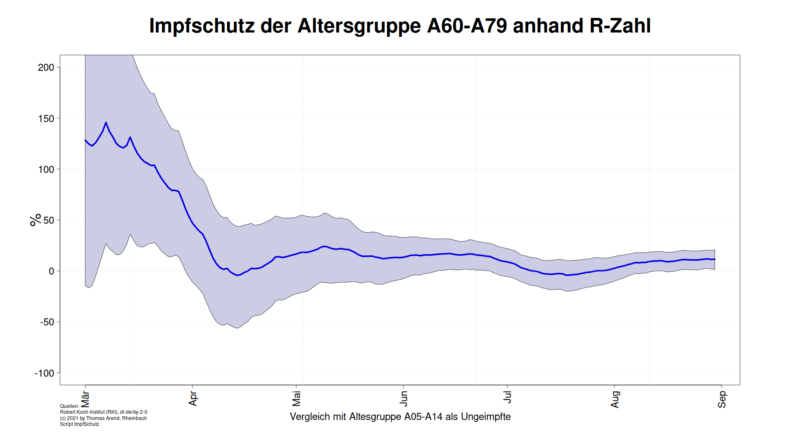
Lassen wir also die Scripte laufen und erhalten für die Regression der R-Zahlen über jeweils sechs Wochen ab 01.03.2021 und dem daraus abgeleiteten Schutz der Impfung für die Altersgruppe A60-A79 und A80+ im Vergleich mit der Altersgruppe A05-A14 folgendes Bild:
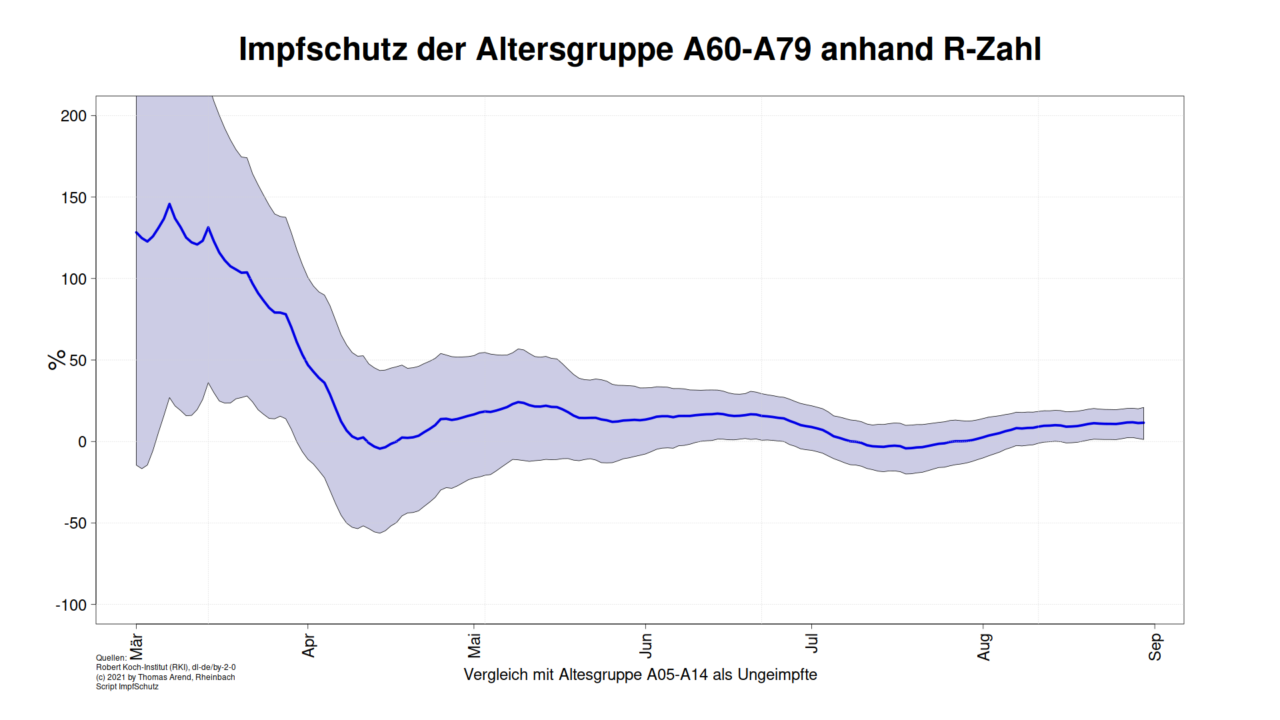
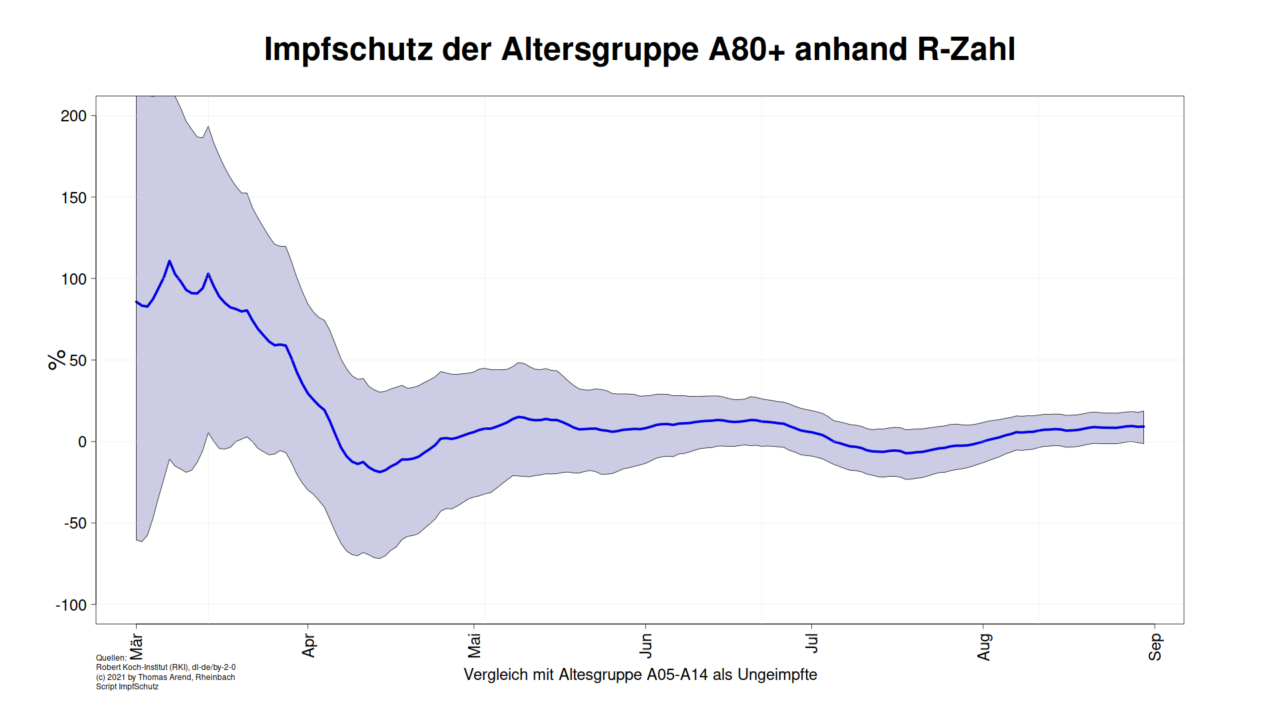
Anmerkung: Das Vertrauensintervall ist im März breiter, weil es umgekehrt proportional zur Impfquote ist. Kleine Impfquote => große Unsicherheit in der Schätzung.
Für den März ergibt sich ein Schutz über 100% bei A60-79. Leider haben wir nur die Impfquote der A60+. Da mit Priorität alte zuerst geimpft wurden, überschätzen wir die Impfquote in der Altersgruppe A60-79. Erst später ergibt sich eine Impfquote von ~84% für die gesamte Gruppe.
Das RKI könnte wirklich bessere Daten liefern. Garbage in, garbage out.
Die R-Zahl unterliegt vielen Einflussfaktoren. In diesem Ansatz werden alle Unterschiede in der R-Zahl der Impfung und dem Impfschutz zugeschrieben, was sicher nicht richtig ist. Die R-Zahlen der Altersgruppen haben sich zu allen Zeiten unterschieden, so dass in diesem Modell auch ein Impfschutz ohne Impfung zu errechnen wäre.
Dafür sind auch unterschiedliche NPI in den Altersgruppen verantwortlich, die wie anhand der Daten nicht raus rechnen können. Kinder sind mit der Altersgruppe A60-A79 in ihren Kontakten und Schutzmaßnahmen nicht direkt vergleichbar. Die Verwendung dieser Altersgruppe ist eine Krücke. Mit Öffnung der Schulen wäre eine höherer Wert für R8t) zu erwarten gewesen, was teilweise der Fall its, Aber auch der Wert der Altersgruppen A60-A79 udn A80+ist erhöht. Aber es gibt keine bessere Vergleichskohorte.
Im März stagnierten die Fallzahlen der A80+ (R ~1), während die Fallzahlen der Altersgruppe A05-A14 stiegen. Ein guter Ansatz hier einen Schutzfaktor der Impfung zu berechnen.
Für den Unterschied können natürlich andere Maßnahmen (mit) ursächlich sein, doch allgemein wird angenommen, dass dies durch die Impfung verursacht wurde.
Später ergibt sich zeitweise ein negativer Schutz. Auch hier überlagern andere Maßnahmen sicher den Schutz und er könnte höher sein, allerdings ist er deutlich niedriger als erhofft. Mit 10% liegt er am unteren Rand einer israelische Studie 39% [CI 95: 9% – 59%]. Damit wäre das Ergebnis nicht völlig unplausibel.
Mit Aufkommen der Variante Delta geht dieser Schutz zurück und sinkt auf ca 10%. In diesem Bereich verharrt er seit Mai 2021.
Im Monat August ergibt sich für die Altersgruppe A60-79 ein Schutz von 11,5% [CI95%: 1,2% – 20,9%] und der Altersgruppe A80+ von 9,2% [CI95%: -1,3% – 18,7%].
Obwohl statistisch nicht signifikant widerspricht dies nicht den Vermutungen, dass der Impfschutz mit der Zeit abnimmt (A80+ wurde vor A60-A79 geimpft). Allerdings beträgt nach diesem Modell der Impfschutz bereits seit Ende April nur etwa 10%. Dies spricht eher dafür, dass die Delta-Variante die Hauptursache für den gesunkenen Schutz vor Infektion ist.
Zwischen Mitte Juni und Mitte Juli dieses Jahres rund 24.000 Corona-Fälle gemeldet, 1.500 davon waren vollständig geimpft. Passt das mit den Berechnungen zusammen?
Ja, wenn bei dieser Zählung die Altersstruktur nicht berücksichtigt wird. Es infizieren sich sehr viel mehr junge, eher ungeimpfte Menschen, als alte, eher geimpfte Menschen. Deshalb ist die einfach Rechnung mit Impfdurchbrüchen nicht richtig.
Fazit:
Für die dritte Welle ergibt sich bei allen Unsicherheiten für den März unter der Alpha-Variante ein Schutz vor Infektion nahe 100%, der aber schon im März abfällt.
Nette Idee, aber mangels guter Vergleichsgruppen, nicht berücksichtigbare Faktoren und schlecht bestimmbaren R-Zahlen und hoher Volatilität der R-Zahl wenig aussagekräftig.
Frage 2: Schützt die Impfung vor Tod?
Nachdem wir nur einen geringen Schutz gegen Infektion errechnen konnten, stell sich die nächste Frage, ob die Impfung vor schwerem Verlauf oder Tod schützt. Zu letzterem führt die Antwort über die Case Fatality Rate (CFR). Dazu müssen wir die CFR der ungeimpften bestimmen und schauen, wie sich die CFR innerhalb einer Altersgruppe mit fortschreiten der Impfung ändert.
Nehmen wir mal an, es gibt keinen Schutz vor Infektion. Dann müssten in einer Altersgruppe Infizierten sich im Durchschnitt entsprechen der Impfquote auf Geimpfte und ungeimpfte aufteilen. Die CFR der Ungeimpften können wir aus ein der Vergangenheit vor der Impfung ermitteln. Sie mag sich mit der Delta-Variante ändern, aber das lassen wir einmal außer acht. Je nach Schutz der Geimpften vor Tod müsste daher die CFR sinken. Dazu vergleichen wir ein „rollende“ CFR mit der CFR für Ungeimpfte und berechnen daraus die CFR der Geimpften. In diesem Modell gibt es 100% Impfdurchbrüche oder 0% Schutz vor Infektion.
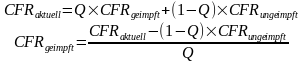
Erweitert um einen Schutzfaktor S vor Infektion sieht die Formel wie folgt aus:
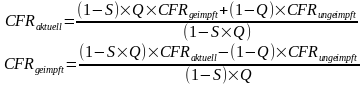
Soweit die Theorie. Jetzt zur Umsetzung.
Als erstes brauche wir eine CFR für Ungeimpfte. Nichts einfacher, als das: Wir nehmen die CFR am Ende des letzten Jahres, als noch niemand geimpft war. Aber schauen wir un zuerst den Verlauf der CFR an. Wir beschränken uns auf die Altersgruppe A60-A79 und A80+, weil es in den anderen Altersgruppe zu wenig Sterbefälle für eine sinnvolle Aussage gibt.
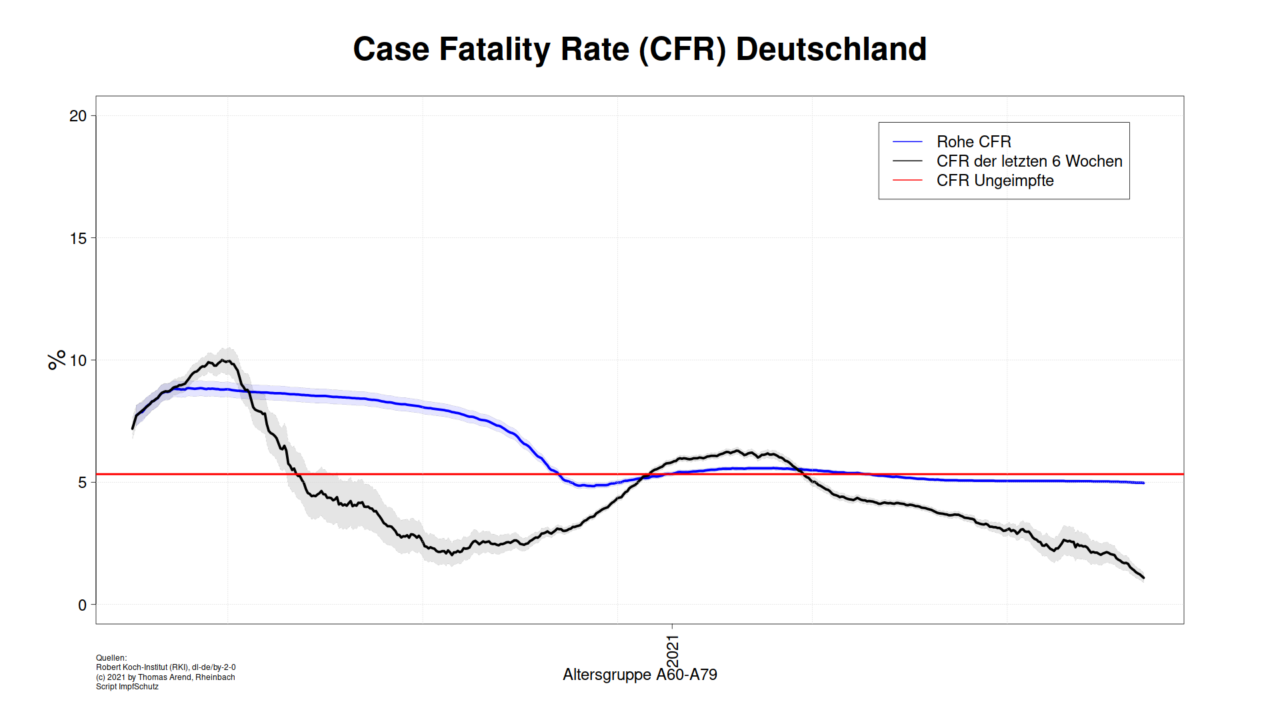
Am Anfang der ersten Welle war die rohe CFR volatil wegen der kleine Todesfallzahle. Deshalb beginnt die Grafik erst mit den 01.04.2020. In der Regel sinkt die CFR zu Beginn einer Welle und steigt nach Überschreiten des Höhepunktes wieder an. Über den Sommer 2020 ist die CFR abgefallen , was verschiedene Ursachen haben kann. In der zweiten und dritten Welle erreicht die CFR nicht mehr die Höhe nach der ersten Welle.
Mögliche Ursachen:
- Durch umfangreiches Testen werden mehr asymptomatische Fälle bei sehr niedrigen Fallzahlen gefunden.
- Durch verbesserte Behandlung der Erkrankten sterben weniger.
- Nicht gemeldete Todesfälle
Seit Ende des Jahres sinkt die rohe CFR und die CFR der letzten sechs Wochen kontinuierlich. Das Argument der umfangreichen Testungen bei kleinen Fallzahlen trägt dieses Jahr nicht. Die CFR ist mit Beginn der Impfung gesunken und die Fallzahlen waren fast 100x höher bei relativ konstanten oder weniger PCR-Testungen, allerdings höheren Schnell-Testungen.
Schauen wir noch auf die Altersgruppe A80+. Der Verlauf der CFR ähnelt dem Verlauf der CFR der anderen Altersgruppen.
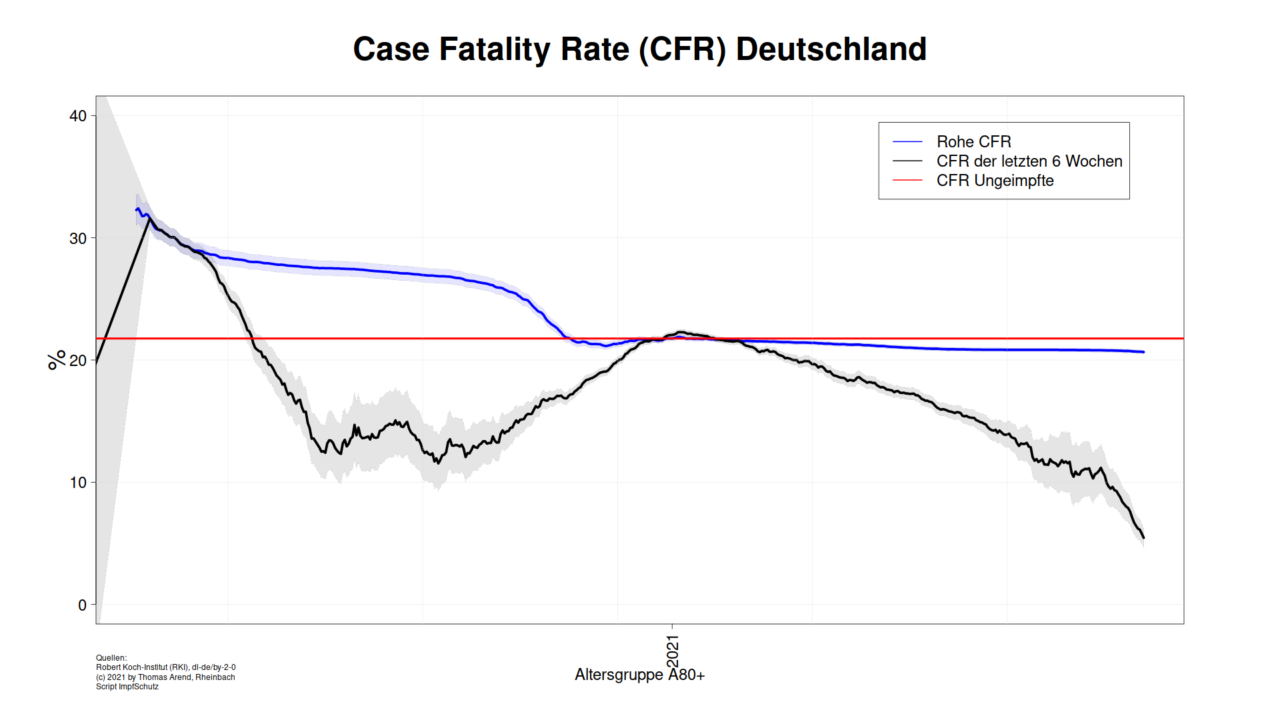
Den Abfall ganz rechts im August 2021 lassen wir unberücksichtigt, seine Ursache liegt im Meldeverzug bei Todesfällen. Diese Todesfälle werden erst in den nächsten Wochen gemeldet.
Überlegungen zu Extremwerten
Bevor wir eine Auswertung der CFR vornehmen, möchte ich ein wir ein paar Extremwerte der obigen Formeln betrachten. Unsere Grundannahmen lautet:
Annahme 1: Das Sinken der gleitenden CFR der letzten 6 Wochen liegt an der Impfung und deren Schutz vor Infektion, schweren Verläufen und Tod.
Annahme 1a: Die Impfung schützt 100% vor Infektion.
In diesem Fall sind keine Geimpften unter den Infizierten und die aktuelle CFR müsste gleich der CFR der Ungeimpften sein. (Siehe Formel mit Schutz). Das ist aber nicht der Fall. Um die CFR der Ungeimpften zu halbieren müsste die Hälfte der Erkrankten Geimpfte mit einer CFR von 0 sein.
Dh., die Annahme 1b, der Schutz vor Infektion ist nicht 100%, können wir verwerfen.
Annahme 1b: Die Impfung schützt zu 100% vor Tod. Dh. CFR geimpft = 0.
Dann können wir aus der 2. Formel den Schutz vor Infektion anhand der aktuellen CFR berechnen.
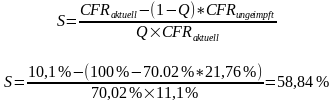
aus der CFR, wenn Impfung zu 100% vor Tod schützt
Aus der 6-Wochen CFR zum 01.08.2021 ergibt sich ein Schutz von
- A60-A79: 46,93% [CI 95%: 18,61% – 64,73%]
- A80+: 58,88% [CI 95%: 37,37% – 73,10%].
Dieses Ergebnis steht nicht in einem logischen Widerspruch zu unseren Annahmen. Vertrauensintervalle mit einer Breite von über 40% sind nicht das Gelbe vom Ei, aber was soll ich machen, wenn die Messwerte stark streuen.
Annahme 1c: Die Impfung schützt nicht vor Infektion.
Dann nehmen wir die erste Formel und erhalten für den Schutz vor Tod
- A60-A79: 79,04% [CU 95%: 64,50% – 93,59%]
- A80+: 69,96% [CU 95%: 55,10% – 84,83%]
Zwischenfazit
Wenn wir keinen Schutz vor Tod haben, haben wir einen hohen Schutz vor Infektion, haben wir keinen Schutz vor Infektion, haben wir einen hohen Schutz vor Tod. Irgendwo in diesem Bereich wir die Wahrheit liegen.
Schutz vor Tod bei geringem Schutz vor Infektion
In der 2. Formel zur CFR haben wir zwei Unbekannte S und CFRgeimpft. Leider fehlt uns eine zweite Formel um eine der Unbekannte zu eliminieren, wie bei der Betrachtung der R-Zahl. Hier ist guter Rat teuer. Das Beste wäre es, wir hätten eine Statistik der Infizierte nach Geimpft und Ungeimpft aufführt – also richtig zählt und nicht schätzt, denn jede Schätzung gibt ihre Fehler weiter.
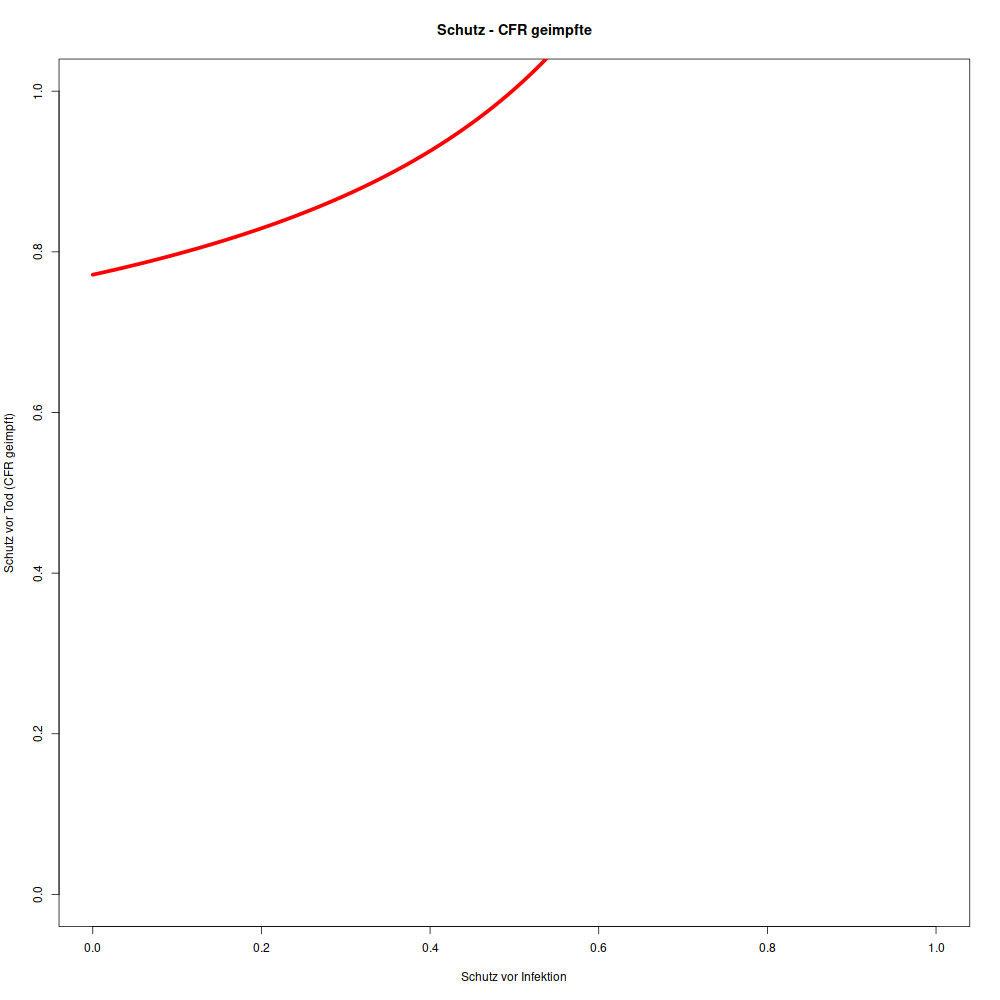
Für die folgenden Grafiken zur CFR für Geimpfte habe ich einfach den Schutz vor Infektion aus der Betrachtung der R-Zahl mit 10% zugrunde gelegt.
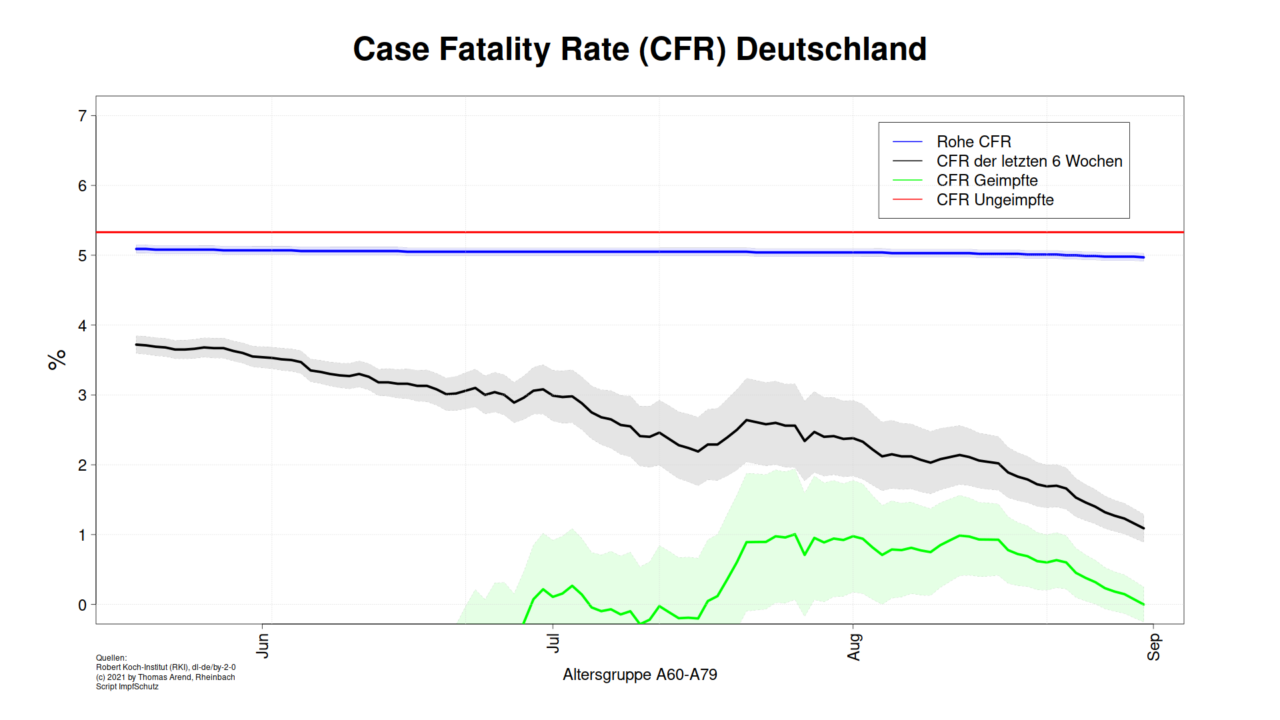
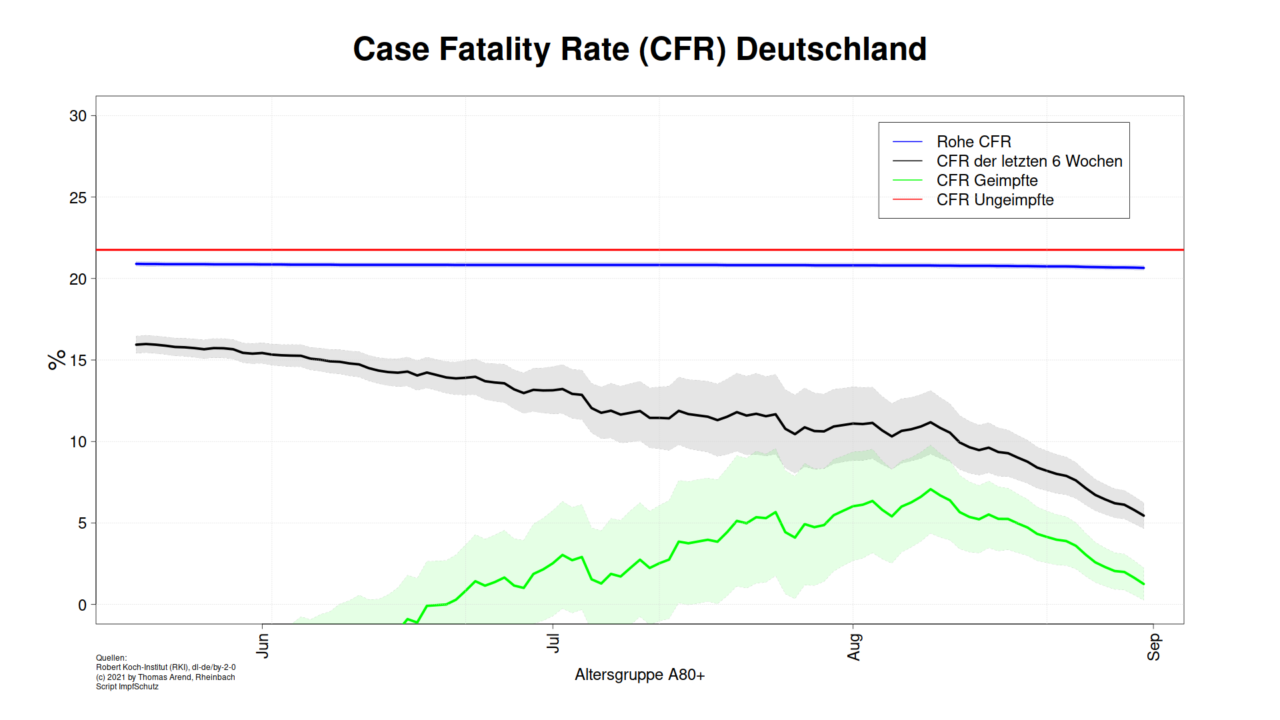
Für die Diagramme habe ich nur den Zeitraum genommen, in dem die ImpfQuote > 20% ist. Am Anfang muss die CFR der Geimpften sogar negativ sein, um die aktuelle CFR bei fester CFR für ungeimpfte zu erreichen. Negative CFR geht (leider) nicht, gestorbene stehen normalerweise nicht wieder auf.
Die gute Nachricht aus der zweiten Formel ist: Wenn der Schutz vor Infektion steigt, sinkt die CFR und damit steigt der Schutz vor Tod.
Fazit
Aufgrund der Daten lässt sich der wirkliche Schutz der Impfung nicht sonderlich genau bestimmen. Vertrauensintervalle von 40% sind nicht gerade ein Traum. Dennoch lässt sich aus den Daten des RKI ein Schutz der Impfung vor Infektion und Tod nachweisen. Trotzdem gibt es zahlreiche Einflussfaktoren, die in den obigen Betrachtungen mangels Daten unberücksichtigt blieben. Allein, dass zeit weise eien negative CFR für geimpfte notwendig ist, um im Modell die aktuelle CFR zu erklären, zeigt, dass noch andere Faktoren eine Rolle spielen. Vielleicht ließe sich das eine oder andere mit einer genaueren Impfquote für die beiden Altersgruppen klären.
ENDE

Neueste Kommentare