Professor Dr. med. Frank P. Meyer schreibt gelegentlich Leserbriefe zum absoluten (AR) und relativen Risiko (RR). Er hat die Unterschiede aber nicht so recht verstanden. Auch Veröffentliochungen anderer Autoren (siehe Links) zeigen, dass die absolute Risikoreduktion und die Anzahl der zu Impfenden um einen Fall zu Vernindern (numbder needed to vaccinate) im Zusammenhang mit Phase 3 Studien nicht verstanden wurde.
In dem Leserbrief Fake News in der Medizin: Relatives Risiko Dtsch Arztebl 2021; 118(35-36): A-1596 geht es um den Artikel Pollack et al.: Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine (NEJM, 10. Dezember 2020) zusammengefasst: „A two-dose regimen of BNT162b2 conferred 95 % protection against Covid-19 in persons 16 years of age or older.“
Das relative Risiko und die relative Risikoreduktion sind für Prof. Meyer Fake News der Pharmaindustrie. Er behauptet: Weil die absolute Risikoreduktion in den Phase 3 Studien zu kleine Werte hat, kommuniziert die Pharmaindustrie statt der absoluten Risikoreduktion die relative Risikoreduktion.
Was ist an dem Vorwurf dran? (Spoiler: Nichts)
Vorweg etwas vereinfachte Theorie an Beispielen.
Ein kleiner Ausflug in die Threorie
Im ersten Beispiel wollen wir russisches Roulette mit verschiedenen Revolvern spielen. Deshalb orientieren stcih die folgenden Betrachtungen an diesem Beispiel.
Sei ni die Anzahl der Kammern in der Trommel eines Revolvers Ri, ki die Zahl der Patronen in einem Revolver Ri
Absolutes Risiko
Dann ist gilt für das absolute Risiko ARi (der Wahrscheinlichkeit, dass sich ein Schuss löst) bei genau einem Schuss zu sterben:
ARi = ki/ni
Absolute Risikoreduktion
Wenn wir zwei Revolver Ri und Rj mit unterschiedlich vielen Kammern und Patronen haben, dann ist die absolute Risikoreduktion (ARRi,j) als die Differenz der beiden Risiken. Im Prinzip die Differenz zwischen den größeren zum kleinerne aslosuten Risisko.
ARRi,j = ARi - ARj = (ki/ni) - (k2/n2)
Bei ARR > 0 wäre das absolute Rissiko gesengt, bei ARR < 0 erhöht und bei ARR = 0 wäre es gleich.
Relatives Risiko
Das relative Risiko (RRi,j) ist definiert als das Verhältnis der beiden AR zueinander:
RRi,j = ARi/ARj = (ki/ni) / (kj/nj) = (ki/kj) * (ni/ni)
Bei RR > 1 wäre das Risiko erhöht, bei RR < 1 gesenkt und bei RR = 0 wären die absoluten Risiken gleich.
Während das absolute Risiko abhängig von der Anzahl der Kammern in der Trommel ist, ist das RR nur abhängig vom Verhältins der Patronen und dem umgekehrten Größenverhältnis der Trommeln. Um es nicht unnötig zu verkomplizieren, nehmen wir Revolver mit gleich großen Trommeln.
Die relative Risikoreduktion (RRR) wird auch Schutz oder Sicherheit genannt und ist definiert als
RRR = 1 - RR
Zusammenhang absolutes Risikoreduktion und relatives Risiko
Wie hängen nun die Absolute Risikoreduktion und das Relative Risiko zusammmen?
ARRi,j = ARi - ARj RRi,j = ARj/ARi => ARRi,j = ARi - RRi,j * ARi = ( 1 - RRi,j ) * ARi = RRRi,j * ARi
D.h. die absolute Risikorreduktion ist proportional zur relativen Risikoreduktion und dem Risiko im Nenner des RR.
Das sollte als theoretische Grundlage ausreichen.
Beispiel 1: Russisches Roulette
Um den Unterschied zwischen absoluter Risiko Reduktion (ARR) und relativer Risikoreduktion (RRR) an einem Beispiel zu erläutern, spielen wir jetzt russisches Roulette.
Zuerst nehmen wir 6-Schüssige Revolver. Die verschiedenen Revolver bezeichnen wir mit Ri, wobei i die Nummer des jeweiligen Revolvers ist. In R1 kommen 2 Patronen, in R2 kommt 1 Patrone.
Das absolute Risiko (oder die Wahrscheinlichkeit) bei einem Schuss aus R1 zu sterben ist 2 / 6 = 0,333, bei R2 ist es 1 / 6 = 0,166.
Die absolute Risikoreduktion (ARR) ist die Differenz dieser beiden Wahrscheinlichkeiten (in %-Punkten. Im folgenden werde ich auf diesen feinem Unterschied nicht weiter hinweisen. Wird subtrahiert oder addiert, ist das Ergebnis in %-Punkten, bei Division oder Multiplikation %).
(2 - 1) / 6 = 1 / 6 = 0,166 = 16,6%
Für das relative Risiko (in %) ergibt sich:
1 / 2 = 0,50 = 50% und für RRR = 1 - RR = 0,5 = 50%
Erhöhung der Patronen
Nun erhöhen wir die Zahl der Patronen. In R3 kommen 3 und in R4 kommen 2.
Das AR bei einem Schuss aus R3 zu sterben ist jetzt 3 / 6 = 0,5; aus R4 ist es 2 / 6 = 0,333.
Die ARR ist wieder 16,7%.
(3 -2 ) / 6 = 1 / 6 ~ 0,167 = 16,7%
Das RR ändert sich jedoch und ist
2 / 3 ~ 0,667 = 66,7% und RRR = 1 - RR = 33,3%
Das heißt die RRR beträgt nur 33,3% statt 50%.
Ich würde daher lieber mit R2 spielen.
Größere Trommeln
Jetzt vergrößern wir die Trommel auf 100 Schuss. In R5 kommen 2 Patronen, in R6 1 Patrone.
Das AR ist 2 / 100 = 0,02 bzw 1 / 100 = 0,01. Die ARR ist somit
0,02 - 0,01 = 0,01 = 1%
Wir sehen, dass die ARR bei gleicher Patronenzahl abhängig von der Größe der Trommel ist.
0,01 / 0,02 = 0,5 = 50%
Die RRR ist wieder 50%. Obwohl das absolute Risiko gesunken ist, bleibt das relative Risiko gleich.
Nun packen wir in eine Trommel etwas mehr Patronen hinein. In R7 kommen jetzt 20 Patronen. Das AR7 ist 20 / 100 = 0,20. Die ARR ist somit
0,2 - 0,01 = 0,19 = 19%
Jetzt erhöhen wir auf 30 bzw 11 Patronen (R8/R9), also um jeweils um 10 Patronen. Das AR ist nun 0,3 bzw. 0,11, Für die ARR ergibt sich
0,30 - 0,11 = 0,19 = 19%.
Was passiert mit dem RR? Bei 20 und 1 Patrone ist es
1 / 20 = 0,05 = 5%
Die RRR ist 1 – RR = 95%. Bei 30 vs 11 Patronen ist das RR
11 / 030 = 0,366 und RRR = 63,3 %
und die RRR beträgt 63,3%.
Die RRR bliebe immer gleich 95% bzw. 63,3%, egal ob wir eine 100-, 1000- oder 10000-Trommel nehmen. Das AR und die ARR sinken, je größer die Trommel ist.
Bevor wir die Frage beantworten, welche Risikoreduktion ist die richtige – Spoiler: Es kommt drauf an –, schauen wir uns ein zweites Beispiel an.
Beispiel 2: Hundebisse
Die Idee mit den beißenden Hunden ist im Ansatz sehr gut, aber nicht ganz präzise zu Ende gedacht. Ändern wir die Idee ein klein wenig ab und präzisieren sie.
Ich versuch es mal anders: mein Risiko während meines Lebens von 1 Hund gebissen zu werden liegt sagen wir mal bei 1%. Wenn man mir nun sagt: „Steck Dir immer Leckerli ein, dann reduzierst Du dieses Risiko um 95%“, dann mag das ja stimmen. Wenn ich daraufhin aber 1/
— 𝖉𝖎𝖊 𝖒𝖆𝖗𝖑𝖊𝖓𝖊 (@diemarlene) September 15, 2021
Nehmen wir an, die Wahrscheinlichkeit bei einer Begegnung mit einem Hund gebissen zu werden ist 1% (absolutes Risiko ohne Leckerli). Also nicht überhaupt einmal im Leben gebissen zu werden, sondern bei einer Begegnung. Das ist keine dramatische Änderung, weil wir die Wahrscheinlichkeit einmal im Leben auf einmal im Jahr, im Monat oder Tag gebissen zu werden umrechnen können. Wenn wir die Zahl der Begegnungen im Leben kennen, könnten wir auch die Wahrscheinlichkeit pro Begegnung ausrechnen. Mit dem Ansatz „pro Begegnung“ sind wir unabhängig von der Person und der unbekannten Häufigkeit der Begegnungen in ein bestimmten Zeitraum. Wir lassen außen vor, dass es Hunde gibt,die häufiger beißen, und Hunde, die überhaupt nicht beißen. Im Mittel beißt ein Hund bei jeder 100-sten Begegnung. Zugegeben etwas häufig, aber darum geht es hier nicht.
Aus einem Versuch wissen wir, dass ein Leckerli das Risiko auf 0,05% (absolutes Risiko mit Leckerli) – also um 95% – senkt. Von 2000 Menschen ohne Leckerlie werden also im Schnitt 20 gebissen. Von 2000 mit Leckerli nur einer.
Oder: Ohne Leckerli werde ich im Schnitt bei jeder 100-sten Begegnung gebissen, mit Leckerli nur bei jeder 2000-sten.
Die ARR wäre 1% – 0,05% = 0,95%. Das relative Risiko wäre dagegen 0,05% / 1% = 0,05 = 5%, die relative Risikoreduktion 1 – RR = 95%.
Begegne ich jeden Monat genau einmal einem Hund, werde ich im Schnitt alle 8 Jahre und 4 Monat einmal gebissen. Mit Leckerli werde ich einmal in 166 Jahren und 8 Monaten gebissen. Ich habe also gute Chancen mit Leckerli im meinem ganzen Leben gar nicht gebissen zu werden.
Nun erhöhen wir die Kontakte auf eine Begegnung pro Tag. Dann werde ich im Schnitt alle 100 Tage oder im Laufe eines 83-Jährigen Lebens etwa 303 mal (ohne Schalttage) gebissen – ohne Leckerli. Mit Leckerli sind es nur 15 Bisse.
Die Differenz (303-15) = 288 Bisse weniger, ist der absolute Schutz, den das Leckerli bietet.
Das relative Risiko 0,05% / 1% = 5% ist unabhängig von der Zahl der Hundekontakte. Jemand mit einem Kontakt pro Monat kann sich ausrechnen, wie viel weniger er mit Leckerli bei wie vielen Kontakten gebissen wird. Das relative Risiko ist nur unabhängig vom Verhältnis der absoluten Risiken gebissen zu werden und damit auch unabhängig von der Person und Verhaltensänderungen, wie arbeiten im Tierheim.
Wie hängt dies mit Phase 3 Studien und dem Impfschutz zusammen?
Woher könnten wir die Wahrscheinlichkeit für einen Hundebiss kennen? Nun wir könnten 40.000 Begegnungen „Mensch – Hund“ organisieren und stellen fest, dass von 20.000 ohne Leckerli 200 Personen gebissen wurden, während von 20.000 mit Leckerli nur 10 Personen gebissen wurden.
Die Risk Ratio, das relative Risiko (RR) „Leckerli vs Kein Leckerli“ beträgt also 10/200 = 5%, die relative Risikoreduktion oder der Schutz ist 1 – RR = 95%.
Wie machen wir es bei Impfstoffen?
Ähnlich aber nicht gleich. Wir impfen 20.000 Menschen und 20.000 Menschen bekommen ein Placebo. Wir wissen gar nicht, wie groß das Risiko für eine Infektion bei einer Begegnung „Mensch – Mensch“ ist. Wir kennen auch die Zahl der Begegnungen nicht. Manche werden mehr Begegnungen, manche weniger haben. Bei den Hunden konnten wir es in einem kontrollierten Versuch testen.
Bei den Hundebissen hätten es auch 100.000 Begegnungen mit 200 zu 10 Bissen sein können, dann wäre zwar das absolute Risiko pro Begegnung auf 0,2% bzw 0,01% gesunken, die RR 5% wäre die gleiche gewesen.
Und das ist der „Trick“ bei Phase 3 Studien.
Dazu nehmen wir an, dass die Menschen sich im Durchschnitt während der Studiendauer ungefähr gleich verhalten. Um das relative Risiko oder die Wirksamkeit der Impfung zu bestimmen, brauchen wir nicht die Zahl der Kontakte, sondern nur die Zahl der Infizierten in den Vergleichsgruppen. 200 vs 10.
Ob die Probanden 1000 ,1 Millionen oder 1 Milliarde Begegnungen hatten, spielt für das relative Risiko keine Rolle. Ohne zu wissen, wie groß das absolute Risiko bei einer einzelnen Begegnung ist, wissen wir, dass es mit Impfung nur 5% des Risikos ohne Impfung ist – oder die Impfung bei einer Begegnung die Wahrscheinlichkeit einer Infektion um 95% reduziert.
Wir können es uns auch so vorstellen, dass wir die Zeit bis zur Ansteckung auf der Zeitachse strecken. Wenn es ohne Impfung bei einer konstanten Inzidenz 100 Wochen oder 2 Jahre bis zu einer Infektion dauert, dauert es mit Impfung 2000 Wochen oder 40 Jahre,wenn die Impfung das Risiko einer Infektion um 95% reduziert.
Die absolute Risikoreduktion im Studienzeitraum spielt dafür kein Rolle. Das absolute Risiko ist proportional zur mittleren Inzidenz im Studienzeitraum. Sie müüste zum Vergleich aut pro 100.000 pro Woche umgerechnet werden. Mehr Bedeutung hat sie nicht. Nichts desto trotz kann man sie berechnen und sie wird auch meist der Vollständigkeit halber angegeben.
Warum wäre eine hohe absolute Risikoreduktion in einer Phase 3 Studie unmoralisch?
Wir können eine hohe ARR erreichen, indem wir die Studie länger laufen lassen. Die ARR wäre maximal, wenn alle aus der Placebo-Gruppe infiziert sind (und es keine natürliche Immunität gibt). Dann wäre die ARR = AR(Placebo) – AR(Geimpf) = 100% – AR(Geimpft).
Bei 5% Infizierten in der Impfgruppe wäre die ARR = 100% – 5% = 95%. Das RR = 5% / 100% = 5% und die RRR = 100% – 5% = 95%. D.h. AAR und RRR wären gleich.
Könnte man machen; aber Aufgabe einer Phase 3 Studie ist, die Wirksamkeit der Impfung nachzuweisen, nicht möglichst viele Infizierte und hohe absolute Risikoreduktionen zu erzeugen.
Dieser Nachweis geht statistisch mit deutlich weniger Infizierten, wie das Bild unter deutlich zeigt. Die Leute nehmen freiwillig an der Studie teil und haben ein Recht darauf nicht unnötigen Risiken unnötig lange ausgesetzt zu werden.
Sobald der statistische Nachweis der Wirksamkeit erbracht oder widerlegt ist, muss die Studie beendet werden. Da die Probanden der beiden Gruppen auch ihr Leben riskieren, wäre es unmoralisch, sie länger als notwendig unter Risiko oder Ungewissheit zu belassen. Ist der statistische Nachweis der Wirksamkeit erbracht, muss den Teilnehmern der Placebo-Gruppe die Impfung angeboten werden.
Da die Teilnehmer ihre Gesundheit riskieren, muss das absolute Risiko der Teilnehmer und die Zeit der Ungewissheit „geschützt oder nicht“ so gering wie möglich gehalten werden. Deshalb dürfen die absoluten Risiken der beiden Gruppen nur so hoch sein, wie es für den Nachweis der Wirksamkeit zwingend erforderlich ist. Die absolute Risikoreduktion darf und kann daher nur sehr gering sein.
Beispiel Studie über für 3 Vaccine
Um das zu illustrieren habe ich drei Vaccine und eine Placebo-Gruppe mit je 1000 Personen – sehr stark vereinfacht – simuliert. (Die Anzahl 1000 Probanden wurde gewählt, damit die Zahlen lesbar in das Diagramm passen.)
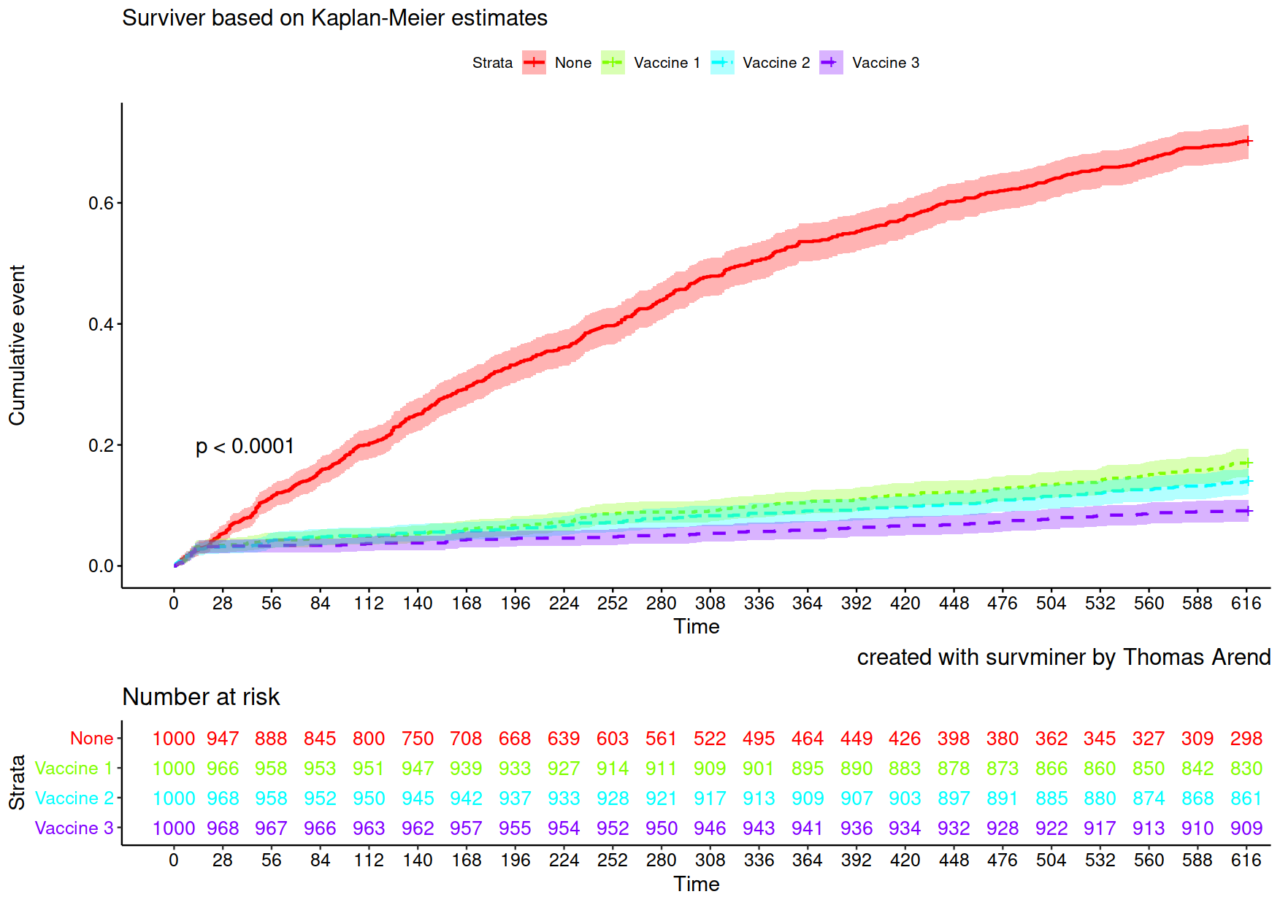
In diese Grafik wird relativ schnell sichtbar, dass die Impfstoffe wirken. Es wäre daher unverantwortlich die Studie beliebig lange fortzusetzen und die Ungeimpften für bessere Daten sterben zu lassen. Wenn der Nachweis der Wirksamkeit eines Medikamentes ausreichend genau erbracht ist, müssen auch die, die bisher mit dem Placebo behandelt wurden, in den Genuss des Medikamentes kommen.
Die Grafik zeigt intuitiv, dass es nicht leicht ist genaue Wirksamkeiten der Impfstoffe zu ermitteln. Um einen signifikanten, nicht zufälligen Unterschied zu sehen, müssten die simulierten Studien sehr lange fdauern. Da spielt aber keine Ethikkommission mit. Wer ethisch verantwortlich handeln will, muss auf Genauigkeit (enge Vertrauensintervalle) verzichten.
Das entsprechende Diagramm der Studie von Pollack findet sich hier.
Studienergebnis nach 112 Tagen
Nehmen wir an, die Studien wären – wie bei BNT162b2 – nach 112 Tagen (16 Wochen) beendet worden. In der Placebo Gruppe hätten 800 überlebt, d.h. 200 wären gestorben. Das ergibt ein AR von 20%. In der Gruppe Vaccine 1 hätten 951 überlebt und 49 wären gestorben. Das AR beträgt 4,9%. Für die ARR ergibt sich 20% – 4,9% = 15,1%.
Das RR beträgt 49 / 200 = 0,245 = 24,5%, die RRR / der Schutz liegt bei 75,5%.
Studienergebnis nach 224 Tagen an.
Nehmen wir an, die Studien wären nach 616 Tagen (32 Wochen) beendet worden. In der Placebo Gruppe hätten 639 überlebt, d.h. 361 wären gestorben. Das ergibt ein AR von 36,1%. In der Gruppe Vaccine 1 haben 927 überlebt und 73 wären gestorben. Das AR beträgt 7,3%. Die ARR beträgt 36,1% – 7,3% = 28,8%.
Das RR beträgt 73 / 361 = 0,202 = 20,2%; die RRR / der Schutz liegt bei 79,8%.
Während der Schutz ungefähr gleich geblieben ist, hat sich die absolute Risikoreduktion nahezu verdoppelt. Für dieses – etwas genauere – Ergebnis mussten aber 161 Menschen der Placebo-Gruppe zusätzlich sterben. Zur Erkenntnis, dass die Impfungen wirksam sind, haben diese zusätzlichen Toten nichts mehr beigetragen. Im Gegenteil, wäre die Studie nach 112 Tagen abgebrochen und die Placebo-Gruppe geimpft worden, würden davon etwa 75% noch leben.
Studienergebnis nach 616 Tagen an.
Blicken wir noch ans Ende der Tabelle auf den Tag 616 (88 Wochen). In der Placebo Gruppe hätten 298 überlebt, d.h. 702 wären gestorben. Das ergibt ein AR von 70,2%. In der Gruppe Vaccine 1 haben 830 überlebt und 170 wären gestorben. Das AR beträgt 17,0%. Die ARR beträgt 70,2% – 17,0% = 53,2%.
Das RR beträgt 170 / 702 = 0,242 = 24,2%; die RRR / der Schutz liegt bei 75,8%.
Damit hätten wir eine sehr hohe absoluten Risikoreduktion auf kosten vieler Probenden, aber keinen Erkenntnisgewinn.
Anm.: Bei Pollack werden nur die Todesfälle 7 Tage nach der zweiten Dosis betrachtet.
Wir sehen, die absolute Risikoreduktion hängt von der Studiendauer an. Dass der Impfstoff, wirkt ist bereits nach 16 Wochen erkennbar.
Warum also noch 16 weitere Wochen warten? Damit eine hohe absolute Risikoreduktion kommuniziert werden kann, die keine Aussage hat?
Und was sagt Professor Meyer?
Die absolute Risikoreduktion (ARR) beträgt also nur 0,70 % (0,74 minus 0,04). Dieser winzige Wert ist natürlich nicht medienwirksam. Also wird zu dem alten Trick der Pharmaindustrie gegriffen und die relative Risikoreduktion (RRR) verkündet und die beträgt tatsächlich 95 % (0,70 bezogen auf 0,74).
Fake News in der Medizin: Relatives Risiko / Dtsch Arztebl 2021; 118(35-36): A-1596 / Meyer, Frank P.
Zwei Impfstoffe lassen sich daher nicht über die absolute Risikoreduktion vergleichen. Eine Studie mit sehr vielen Teilnehmern erreicht sehr viel schneller die erforderliche Zahl an Infizierten, bei der abgebrochen werden kann, als eine Studie mit weniger Teilnehmern, die dafür länger laufen muss.
Die Studie mit vielen Teilnehmern hätte logischerweise ein viel kleineres absolutes Risiko und eine viel kleinere absolute Risikoreduktion. Welche Impfung die bessere ist, lässt sich anhand der absoluten Risikoreduktion nicht entscheiden.
(Dass der Schutz nach 224 Tagen höher als nach 112 Tagen ist, liegt daran, dass in der Simulation der Schutz nicht sofort nach der Impfung vorhanden ist. Je länger die Studie dauert, desto geringer wird der Effekt des nicht sofortigen Impfschutzes. Bei Pollack wurde daher nur das Outcome 7 Tage nach der zweiten Dosis genommen um den Impfschutz zu bestimmen. Das habe ich mir hier erspart.)
Number Needed to Vaccinate (NNV)
Die number needed to treat (NNT) oder to harm (NNH), to test (NNT) oder hier speziell die number needed to vaccinate (NNV) ist ein durchaus gängiger Parameter Maß in der Statistik. Sie bestimmt, wie viele Personen mit einem neuen Mittel oder einer neuen Methode behandelt werden müssen, um ein Ereignis (Infektion, Todesfall, …) zu verhindern. Die number needed to test gibt zum Beispiel an, wie viele Frauen zur Mammografie gehen müssen, um eine Frau mit Brustkrebs zu finden.
Professor Meyer berechnet in seinem Leserbrief die Anzahl der Personen, die sich impfen lassen müssen, um eine Infektion zu verhindern. Ebenso bei Brown Outcome Reporting Bias in COVID-19 mRNA Vaccine Clinical Trials [4].
Es werden also nicht 95 von 100 Geimpften geschützt, sondern man muss 143 Personen impfen, um einen (1) zusätzlichen Coronafall zu verhindern (100 : 0,70 = 143).
Fake News in der Medizin: Relatives Risiko / Dtsch Arztebl 2021; 118(35-36): A-1596 / Meyer, Frank P.
Ob Professor Meyer sich dies selbst zurecht gelegt, von Professor Homburg auf Twitter übernommen hat , bei Brown oder andern Publikation entnommen hat, entzieht sich meiner Kenntnis, denn er gibt keine Quelle an. Weitere Artikel, die ich dazu gefunden, habe ich unten in den Links angefügt.
Alle diese Berechnungen der NNV übersehen den Zeitbezug der ARR. Selbst wenn die absolute Risikoredunktion und die Vergleichbarkeit zwischen den verschiedenen Studien kritisch diskutiert wird, habe ich keine Befürworter der Angabe der ARR oder NNV in einem Studienportokoll gefunden, der erkannt hat, dass die erste bereits im Design der Studie angelegt ist, abhänig von Inzidenz und Studiendauer und die NNV somit völlig aussagelos ist.
Seine Ausführungen zum absoluten vs relativen Risiko sind schon seit Monaten widerlegt.
Das AR 0,74% für die Placebo-Gruppe und 0,04% für die Impfgruppe hat einen Zeitbezug: Es ist das Risiko sich in der Studiendauer (112 Tage) zu infizieren, nicht das Risiko sich irgendwann zu infizieren. Das Risiko der Infektion besteht über die Studie hinaus fort, die Gefahr ist nicht mit Studienende beseitigt.
0,74% ist die Wahrscheinlichkeit eines Probanden der Placebogruppe innerhalb der Studiendauer zu infizieren.
Präzise wäre daher die Angabe: p=0,007/112d Tage oder p=0,00006/d.
Wenn wir AR pro Tag berechnen könnten – vielleicht – unterschiedliche Studien vergleichbar werden. Schauen wir, wass dann aus der NNV wird.
Da die Studie 112 Tage dauert, wäre das AR pro Tag für die Placebo-Gruppe 0,74% = 112 = 0,006% und für die Impfgruppe 0,00036%. Die ARR wäre 0,00625% und die NNV wäre 16.000. Kurz es müssten 16.000 geimpft werden, um eine Infektion an einem Tag zu verhindern.
Moment? MWir ahben die Eingeiten vergessen. Mit Einheiten lautet das Ergebnis präzise 1 Person / (0,00006 / Tage) = 16.000 Tage * Person. Das ist aber nicht die NNV.
Das ist doch etwas seltsam. Es hat schon seinen Grund, warum man Einheiten in Berechnungen immer mitschleppen soll.
Und was ist mit dem relativen Risiko?
Das relative Risiko (RR) oder englisch Risk Ratio, besser übersetzt das Risikoverhältnis, ist einheitenlos. [a Personen / 112 Tage] / [ b Personen / 112 Tage] = a / b.
Beispiel
Bei einer komplizierten Operation sterben im Schnitt 100 von 1000 Personen. Das absolute Risiko ist 100 / 1000 = 10%. Hier gibt es keien versteckten Zeitbezug. Es gilt pro einer Operation, Bruchteile nicht möglich.
Ein neues Medikament wird getestet. Bei 200 Operationen sterben im Test 5 Personen. Das absolute Risiko beträgt daher 5 / 200 = 2,5%. Während die ARR 7,5%-Punkte beträgt, beträgt das relative Risiko RR 2,5% / 10% = 25% und die RRR 75%.
Um einen Todesfall zu verhindern, müssen 1 [Person] / ARR = 1 / 7,5% ~ 13,3 < 14 Personen mit dem neuen Medikament behandelt werden. (Es wird immer auf die nächste ganze Zahl aufgerundet)
Gegenrechnung: Bei 13,3 Personen hätten wir mit der alten Methode 1,3 Sterbefälle, mit dem neuen Medikament 0,3. Da 1,3 – 0,3 = 1 sind, verhindern das Medikament einen Todesfall auf 14 Operationen.
Anm.: Insbesondere bei Vorsorgeuntersuchnungen stellt sich die Frage: Wie viel kostet es einen Todesfall zu verhindern oder einen Brustkrebs zu entdecken? Lohnt sich das? Wie viel investieren wir in Sicherheitstechnik in Autos, um einen bei einem Unfall einen (schwer) Verletzen oder Verunglückten zu verhindern? Wie viele Airbags müssen wir in Autos einbauen, damit einer ausgelöst wird?
In den obigen, simulierten Studien hätte Professor Meyer nach 112 Tagen 6,6 < 7 als die Anzahl zu Impfender um einen Fall zu verhindern ermittelt, nach 224 Tagen wäre er auf 3,5 < 4 gekommen.
Die Anzahl der zu Impfenden ist daher nicht aus der ARR der Studie zu berechnen. Sein Vorgehen liefert keinen statistisch sinnvollen Parameter, wenn man davon absieht zu sagen: Um in der Studiendauer einen Fall zu verhindern, hätte man in der Placebo-Gruppe 143 impfen müssen. Bei höherer Inzidenz wäre es weniger gewesen.
Ausflug Studiendesign
Die number needed to test oder das absolute Risiko hat natürlich seine Bedeutung bei der Bestimmung der Anzahl der Probanden in der Studie.
Zuerst muss festgelegt werden, mit welcher Genauigkeit der Schutz bestimmt werden soll. Z.B. ob er auf 1%-, 5%- oder 10%-Punkte genau bestimmt werden soll. Möchten wir ein Vertrauensintervall 95% von +/- 5%-Punkten, ergibt sich, dass wir etwa 400 Infizierte „benötigen“. D.h. wir brechen die Studie ab, wenn 400 Infiziert sind.
Nun muss die Dauer der Studie festgelegt werden. Nehmen wir 16 Wochen, denn die Zeit drängt.
Jetzt benötigen wir noch die Inzidenz in der Population um Zahl der Probanden für die Studie zu bestimmen. Nehmen wir einfach mal 50 pro Woche pro 100.000 Einwohner. Bei 400 Infizierten und 16 Wochen brauchen wir 25 Infizierte pro Woche, also kommen wir mit 25 / (50 / 100000) = 50.000 Probanden aus, die wir ungefähr auf zwei Gruppen aufteilen.
Damit haben wir auch das AR über alle Probanden festgelegt, denn wir brechen ab, wenn die 400 Infizierten vor Ablauf der 16 Wochen erreicht werden. Die AR beträgt 400 / 50.000 = 0,8%. Wenn sich niemand in der Impfgruppe infiziert, beträgt das maximale AR in der Placebo-Gruppe 1,6%.
Diese 1,6% sind zugleich die maximale ARR, die in der Phase 3 Studie möglich ist. Da sich auch einige aus der Impfgruppe infizieren werden, ist die zu erwartende AAR < 1,6%.
Wir sehen, diese maximale ARR ist bereits im Design festgelegt und keine Erkenntnis aus der Studie.
Unterschied Operationen vs Impfung
Schlussspurt:
Im obigen Beispiel zur NNT haben wir einen definierten Fall ohne Zeitbezug: Eine Operation.
Ebenso im ersten Beispiel mit den Hundebisse, da war es eine Begegnung. BTW: Bei 105 < 106 Begegnungen muss ein Leckeli mitgenommen werden, um einen Biss zu verhindern.
Bei der Impfung haben wir jedoch keine klar definierten Ereignisse, wir kennen die Zahl der Begegnungen in der Bevölkerung nicht, sondern am Ende nur die Anzahl der geimpften und ungeimpften Infizierten im Zeitraum der Studie.
Die Geimpften / Ungeimpften entsprechen unseren Trommeln im Revolver, die Chance sich zu infizierten der Zahl der Patronen. Wenn wir mit unserem Revolver immer wieder schießen, werden wir irgendwann einen Schuss lösen.
Die Wahrscheinlichkeit, dass sich ein Schuss löst, geht gegen 1.
Die Wahrscheinlichkeit sich (nach der Studie) zu infizieren geht ebenso gegen 1, wenn die Zeit gegen unendlich geht. Aber während sich unter den Ungeimpften in einem Zeitabschnitt 20 infizieren, infiziert sich bei den Geimpften im gleichen Zeitabschnitt nur einer.
Oder kurz: Alle, wenn wir so viele Infektionen so lange wie möglich verhindern wollen.
Zum Schluss noch ein Ergebnis ausgedachter Teste zur Anschauung.
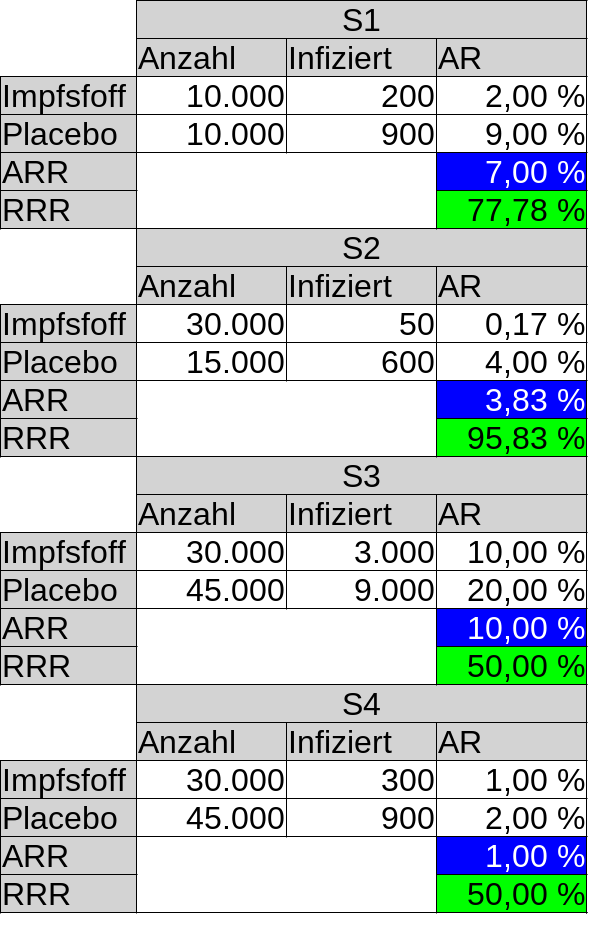
Mein Tipp: Nehmen Sie den Impfstoff aus Studie S2, auch wenn die ARR deutlich kleiner als bei S1 und S3 ist.
Fazit
Mathematische Dilettant*Innen mit Professoren-Titel sollten sich nicht aufs Glatteis der Statistik begeben.
Links:
- Klaus-Dieter Kolenda
Wie wirksam sind die Covid-19-Impfstoffe?
29. Mai 2021↗ - Piero Olliaro, Els Torreele, Michel Vaillant
COVID-19 vaccine efficacy and effectiveness—the elephant (not) in the room
Open AccessPublished: April 20, 2021 DOI:https://doi.org/10.1016/S2666-5247(21)00069-0 - Polack FP Thomas SJ Kitchin N et al.
Safety and efficacy of the BNT162b2 mRNA COVID-19 Vaccine.
N Engl J Med. 2020; 383: 2603-2615 - Ronald B. Brown
Outcome Reporting Bias in COVID-19 mRNA Vaccine Clinical Trials
Medicina 2021, 57(3), 199; DOI:https://doi.org/10.3390/medicina57030199

Neueste Kommentare