Zeitreihen vergleichen

Oft werden von Hobbystatistikern wie mir, Zeitreihen miteinander verglichen und die Korrelation hergestellt. Auch Professor Kuhbandner ist so ein Hobbystatistiker, wie ich schon mal erklärt habe. Nur: Zeitreihen mit einer Tendenz korrelieren immer. Schauen wir uns man drei simulierte Zeitreihen an.

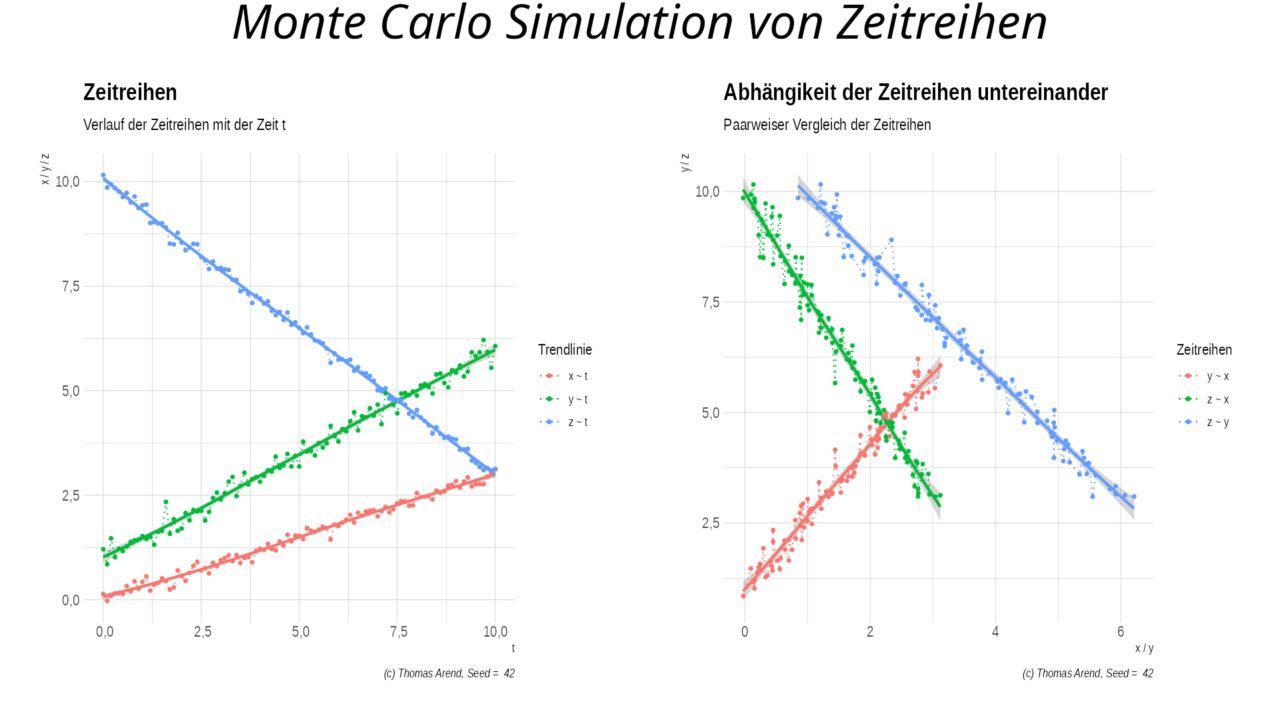
Drei (simulierte) Zeitreihen (links) und ihr paarweiser Vergleich (rechts)

Zwei Zeitreihen haben steigende und eine Zeitreihe hat fallende Tendenz. Wie zu erwarten gibt es auch im paarweisen Vergleich eine Korrelation zwischen den Zeitreihen. Das beweist somit nichts.

Auf den ersten Blick ist kein Unterschied zwischen den Zeitreihen zu erkennen. Aber wenn es einen Zusammenhang gibt, sollte mit dem Wert der eine Zeitreihe auch der Wert der andern Zeitreihe steigen. Also bilden wir die Differenz der Werte zwischen zwei aufeinanderfolgenden Zeitpunkten: x´(ti) =x(ti+1) – x(ti) .

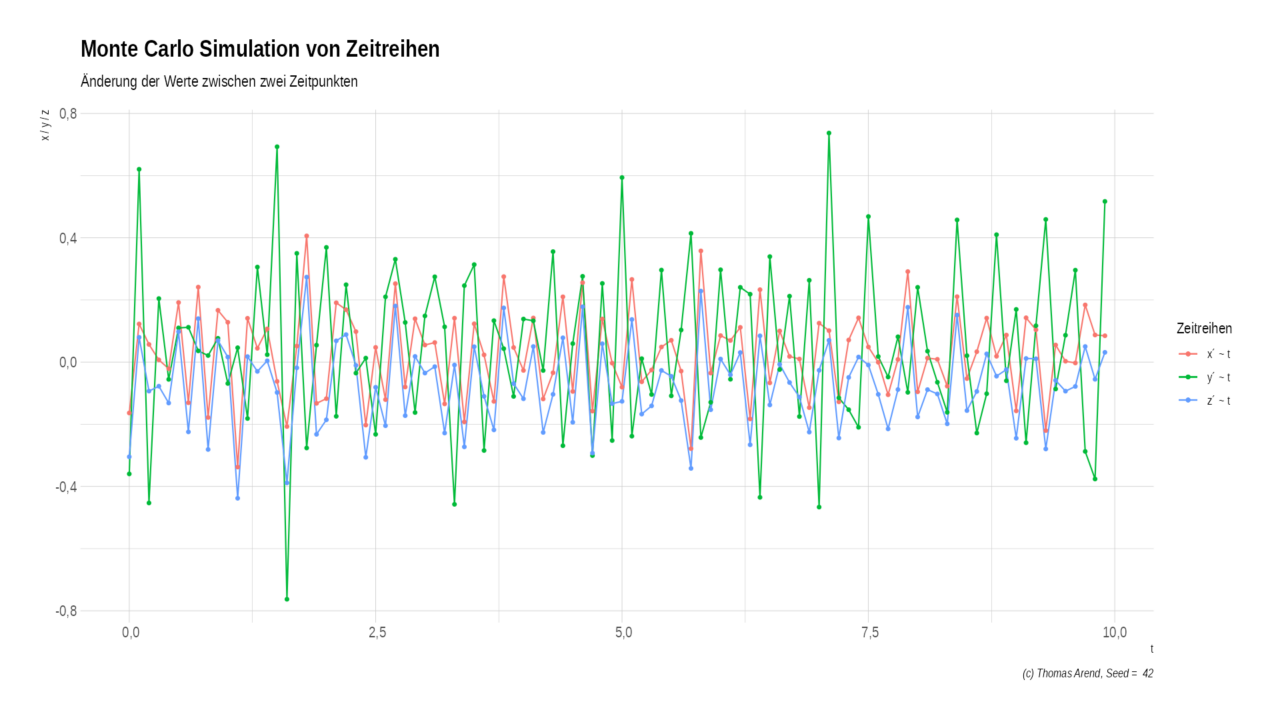
Differenz der Werte zwischen einem Zeitpunkt und dem nächsten Zeitpunkt

In der Zusammenschau sieht das chaotisch aus. Aber wenn wir die y´-Linie weg lassen, wird das Bild klarer.

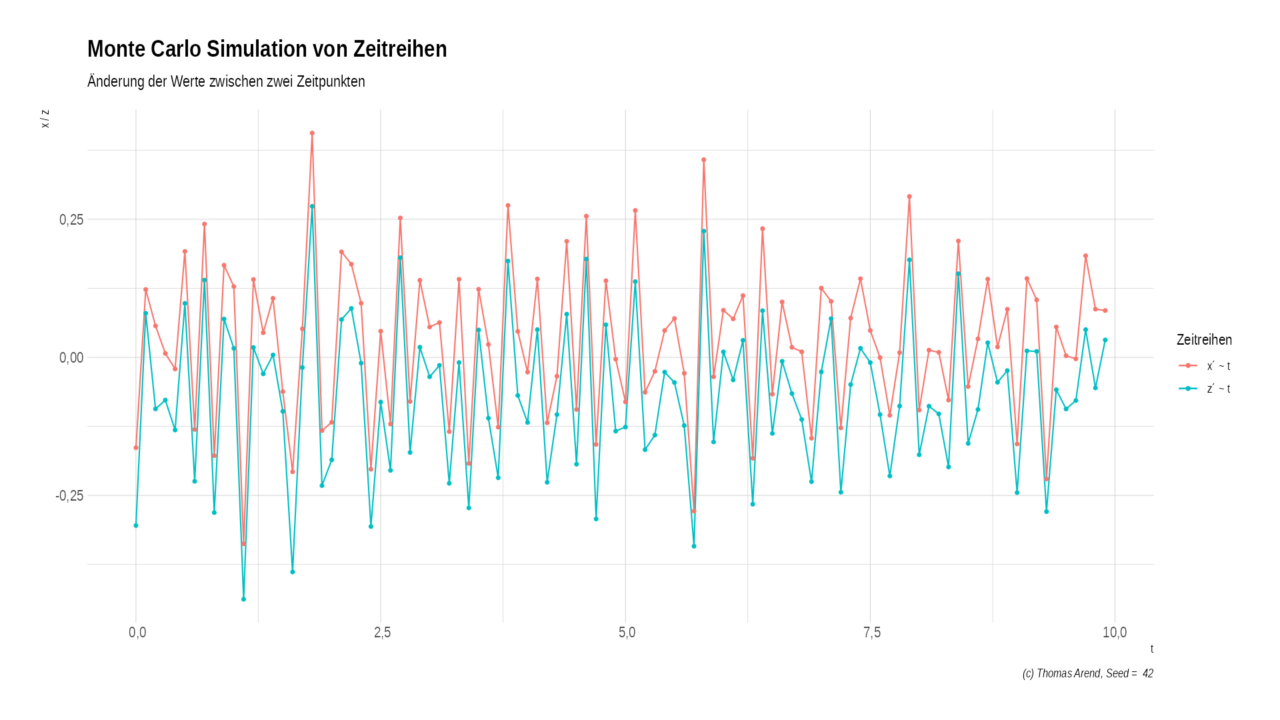
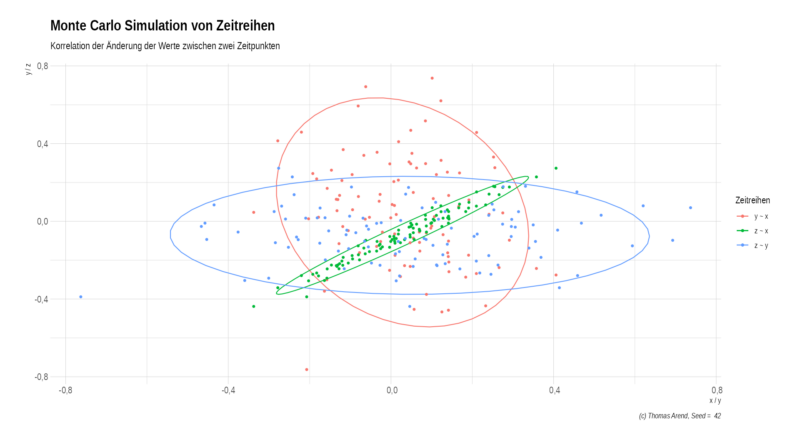
Die Differenz zwischen zwei Zeitpunkten von x und z

Hier wird das Bild schon klarer. Jetzt tragen wir die Änderungen noch in ein Scatterplot und nehmen y´ wieder hinzu.

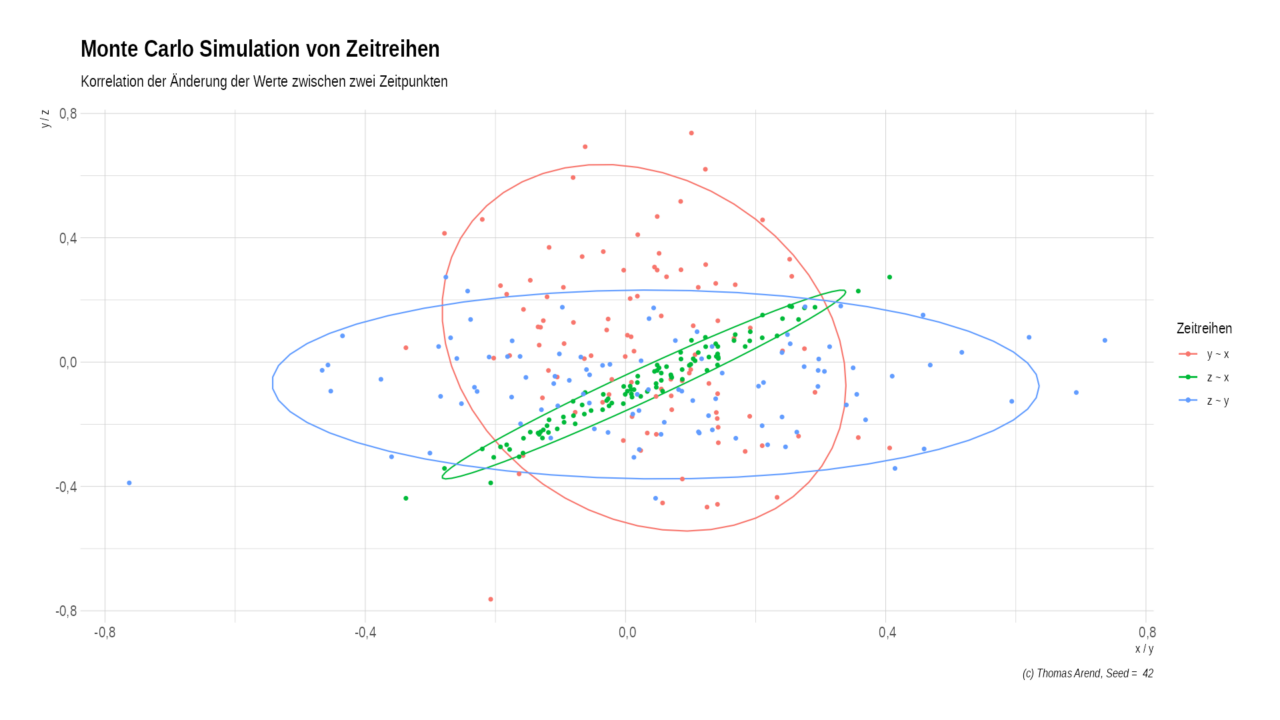
Paarweiser Vergleich der Differenzen der Werte zwischen zwei aufeinanderfolgenden Zeitpunkten

In diesem Bild wird klar: Nur die Änderungen zwischen z und y korrelieren miteinander. Dies wird auch durch die Korrelationskoeffzienten klar.

PaarungKorrelationskoeffizient
y ~ x0,9680523
z ~ x0,9720151
z ~ y0,9818492
y´ ~ x´0,02702575
z´ ~ x´0,9626196
z´ ~ y´0,0008653215
Tabelle der Korrelationskoeffizienten

Während alle Zeitreihen untereinander sehr gut korrelieren, korrelieren nur die Differenzen zwischen zwei aufeinanderfolgenden Zeitpunkten des Paares x und z.

Das ist nicht weiter verwunderlich, weil ich die Streuung der Zeitreihen x und z stärker miteinander gekoppelt habe, als y und z. x und y sind völlig abhängig voneinander.

TP = seq(from = 0, to = 10, by = 0.1)

E1 = rnorm(length(TP), 0, 0.1)
E2 = rnorm(length(TP), 0, 0.2 )

X = TP * 0.3 + E1
Y = TP * 0.5 + 1 + E2
Z = - TP * 0.7 + 10 + E1 + E2/10

ZR <- data.table (
      t = TP
      , x = X
      , y = Y
      , z = Z
)

Und nun schaue wir und das in freier Wildbahn an.

Aktienindizes

Wir nehmen dau die Aktienindizes DAX, Euro STOXX 50E (E50) und Dow Jones Industrial Average (DJI). Die Daten bekommen wir von Yahoo. (Leider gibt es bei DJI keinen CSV-Download Butten, aber die HTML-Tabelle reicht uns.

Zusammenhang der Schlusskurse DAX und Dow Jones Industrial Average
Zusammenhang der Schlusskurse DAX und Euro STOXX 50E
Zusammenhang der Schlusskurse Dow Jones Industrial Average und und Euro STOXX 50E

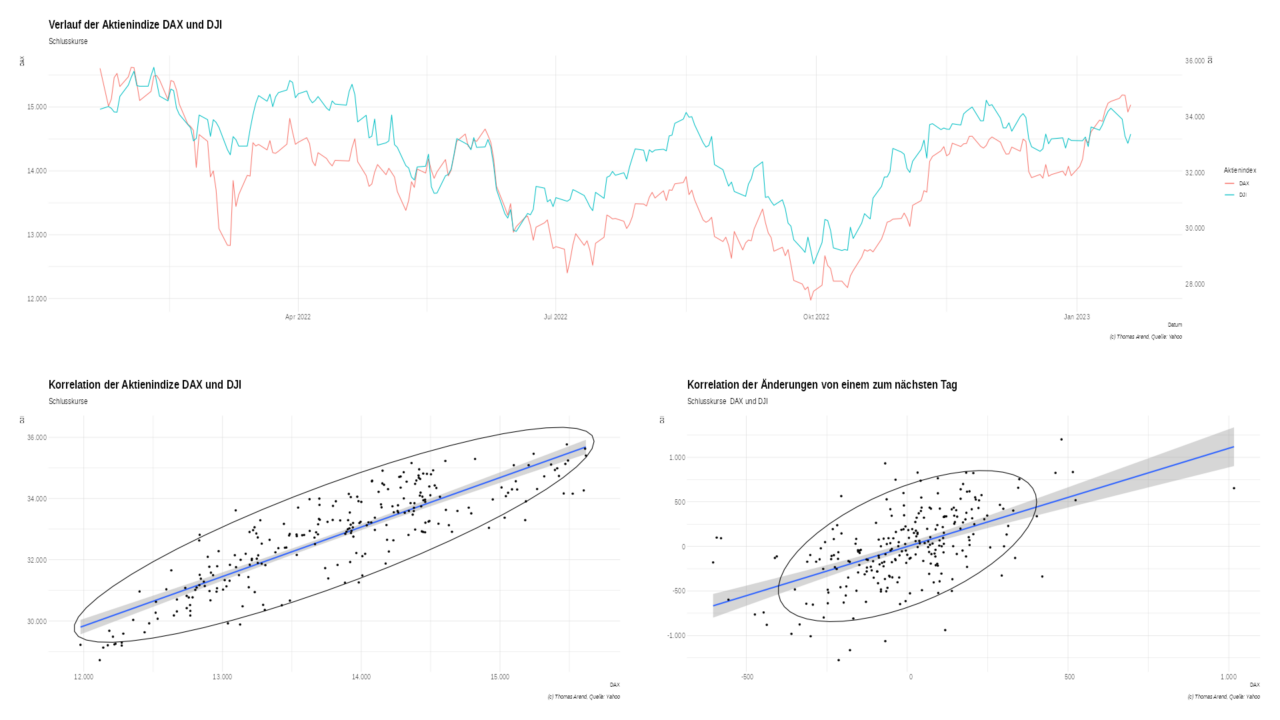
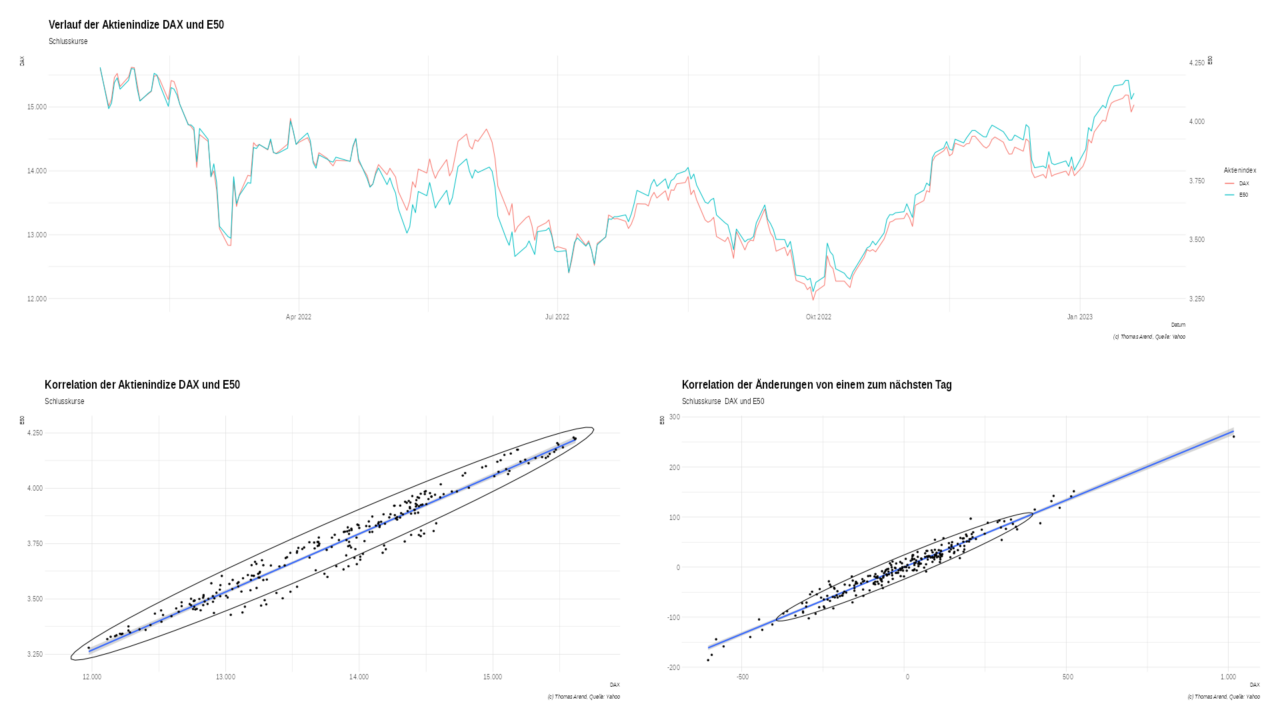
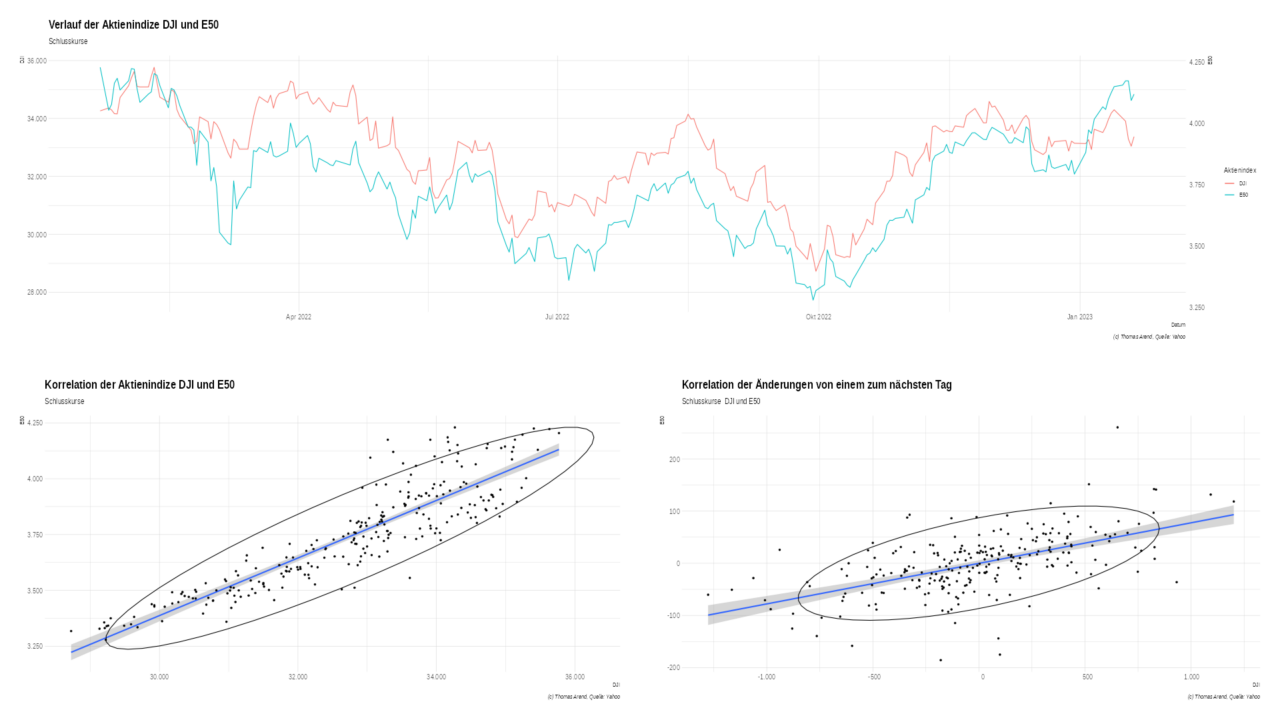
Während es eine starke Korrelation zwischen DAX udn E50 gibt, ist die Korrelation des DJI zu den anderer beiden geringer. Insbesondere bei den Differenzen zwischen den Tagen ist die Korrelation geringer.

Paarung (Formel)R² SchlusskurseR² Tagesdifferenz
DJI ~ DAX0,74833890,3036658
E50 ~ DAX0,94777210,9552755
E50 ~ DJI0,80119470,3267075
Korrelationen der Paarungen der Aktienindizes

Insgesamt hängen korrelieren die Akteinkurse miteinander. Was zu erwarten war. Interessant ist, dass die Kursentwicklung von einem Tag zum nächsten nicht so stark korreliert.

Das ist nur ein Beispiel. Daraus Schlussfolgerungen für den Aktienkauf zu ziehen, könnte teuer werden.

Fazit

Immer, wenn jemand zwei Zeitreihen direkt miteinander vergleicht ohne die Differenzen von einem Zeitpunkt zum nächsten zu betrachten, aufhören weiter zu lesen und das Papier in die Tonne drücken.

Schlagwörter