Roulettestrategien widerlegen

[vgwort line=“59″ server=“vg08″ openid=“de1942eee65247e799ba1deb4596af77″]

Immer wieder werden angebliche Gewinnstrategien in den Raum geworfen. Während ich diesen Artikel schreibe, findet eine angeregte Diskussion auf Geizhals.de statt.

Mathematische, wissenschaftliche korrekt formulierte Beweise gegen die Gewinnstrategien beim Roulette haben den Nachteil, den meisten unverständlich zu sein. Auf der Suche nach einem Beweis, dass das Martingalespiel oder Verdopplungssystem nicht funktionieren kann, stieß ich auf ein Skript des Institutes für Statistik der Ludwig-Maximillian-Universität. Wenn die mathematische Denkweise nicht zur ersten oder zweiten Natur geworden ist, erfordert es sehr viel Zeit die abstrakten Ausführungen zu verstehen. Deshalb versuche ich es einfacher, weniger abstrakt – populärwissenschaftlich, aber durchaus begründet und präzise.

Die Betrachtungen setzen eine perfekte Roulette voraus. Kesselgucken funktioniert nicht. Alle Zahlen von 0 bis 36 sind exakt gleich wahrscheinlich.

Geschichtslosigkeit des Zufalls

Bevor wir uns den Prüfungen der Gewinnstrategien widmen, möchte ich einige Worte zur Geschichtslosigkeit des Zufalls verlieren. Hin und wieder findet man in Foren die Bezeichnung scheinbar gedächtnisloser oder geschichtsloser Zufall. Sogar Glaubensbekenntnisse zur Zwei-Drittel-Regel lassen sich finden. Es erzeugt immer wieder Verwunderung, dass mathematische Vorhersagen eines statistischen Verhaltens sich mit gewissen Toleranzen erfüllen, obwohl die Zufallsereignisse angeblich kein Gedächtnis haben. Wie kann so etwas möglich sein? Wo eine Wirkung, ein Muster ist, muss eine Ursache sein!

Vor weiteren Betrachtungen ist es mir wichtig, die Bedeutung des Begriffes „Geschichtslosigkeit“ zu klären, um dem esoterischen Brimborium, das um irgendwelche Muster oder Folgen gemacht wird, das Genick zu brechen.

Auch wenn die Größe des Universum für folgendes Beispiel nicht ausreicht um es praktisch umzusetzen, verdeutlicht es doch, dass eine Suche nach Serien, Ausgleich oder ähnliches Unfug ist. Um dies zu zeigen, lade ich zu folgendem Gedankenexperiment ein.

Am Tisch 1 der Spielbank Bad Homburg werden pro Tag zwischen 300 und 500 Spiele gespielt. Nehmen wir an, es sind immer 400 Spiele. Statt 400 mal eine Zahl mit der Roulette zu bestimmen, könnten wir alle Permanenzen auf einzelne Lose schreiben[ref]Wir schreiben natürlich nicht per Hand, sondern nehmen einen PC mit Drucker und schreiben ein Programm, in dem 400 For-Next-Schleifen, die alle die Zahlen von 0 bis 36 durchlaufen, ineinander geschachtelt sind. In der Innersten Schleife steht der Befehl, der die Zahlen eines Abend auf eine Seite druckt. So sind wir sicher, keine Kombination zu vergesssen.[/ref], sie in eine Urne legen und eine Glücksfee bitten ein Los zu ziehen. Die Glücksfee öffnet das Los, hält aber die Zahlen streng geheim. Sie liest die nächste Zahl immer erst vor, nachdem die Spieler für den nächsten Coup gesetzt haben. Am Ende des Abends legt die Glücksfee das Los in die Trommel zurück. Am nächsten Tag zieht sie wieder ein Los. Sie kann das Los des vorherigen Tages wieder ziehen, aber das ist extrem unwahrscheinlich, 1 zu 37⁴⁰⁰.

Da alle Zahlen auf einmal gezogen werden, gibt es keine Geschichte zwischen den Zahlen auf einem Los. Jede Folge von 400 Zahlen zwischen 0 und 36 ist gleich wahrscheinlich. Jegliche religiöse oder esoterische Spekulation über Gesetze der Musterbildungen, Serien oder Ausgleich innerhalb eines Loses – einer Permanenz – ist Unfug. Unter allen möglichen Permanenzen über 400 Coups sind so schöne wie 37 mal „0“. 37 mal „36“ oder „0-1-0-1-0-1-…-0-1“. Ihre Wahrscheinlichkeit ist jedoch genauso gering – oder groß – wie die aller anderen, weniger schönen. Es gibt 36*400 „gestörte“ Permanenzen, die aus 399 mal „0“ und einer beliebigen weiteren Zahl bestehen. Die weniger „schönen“ Permanenzen sind zwar in der Mehrheit, jede einzelne ist genauso wahrscheinlich wie 400 mal „0“.

Neues Spiel neues Glück. Eine Zahl muss nicht an einem Abend gezogen werden. Mit 0,06434% ist die Wahrscheinlichkeit, dass eine beliebige Zahl nicht gezogen wird sogar sehr hoch. Sei kommt an 6 von 10.000 Abenden vor.

Ziehungen mit Geschichte, ein kurzer Exkurs

Das Gesetz der kleinen Zahlen, Zwei-Drittel-Gesetz oder Gesetz des Drittels ist ein Satz aus der Stochastik, der einen Sonderfall der Poisson-Verteilung beschreibt. Eine der Voraussetzungen ist die Geschichtslosigkeit der Zufallsereignisse. Das Gesetz der kleinen Zahlen besagt, dass in 37 Coups 13 bis 14 Zahlen[ref]Genau sind es 37*(36/37)³⁷ ~= 37*0,3629 = 13,43 [/ref] nicht gezogen werden. Eine Voraussetzung für dieses Gesetz ist, dass die Ziehungen geschichtslos sind. D.h. die nächste Ziehung weiß nicht, was vorher gezogen wurde. Nun ist es nicht so, dass die Roulette gewisse Zahlen zieht oder nicht zieht, damit das zwei Drittel-Gesetz eingehalten wird, sondern es wird eine Zahl gezogen, weil die Roulette nicht weiß, dass sie schon gezogen wurde.

Wenn die Geschichts- oder Gedächtnislosigkeit des Zufalls so wichtig ist, was wäre dann ein Zufall mit Gedächtnis?

Nehmen wir eine Lotto Ziehung (6 aus 49 mit Zusatzzahl). Es werden hintereinander sieben Kugeln gezogen. Jede Kugel wird der Urne entnommen und nicht wieder zurück gelegt. Keine Kugel kann daher zweimal gezogen werden. Würden wir 49 aus 49 Kugeln ziehen – eine Permutation der Länge 49, dann kommt jede Zahl genau einmal vor. Das Gesetz der kleinen Zahl gilt nicht, denn die Urne „kennt“ die Geschichte der Ziehung. Sie weiß zwar nicht die Reihenfolge der Zahlen, doch sie „merkt“ sich die gezogenen Zahlen. Die Roulette hat diese Möglichkeit nicht.

Das Gesetz der kleinen Zahlen ist – zusammen mit anderen Voraussetzungen – eine Folge der Geschichtslosigkeit, auch wenn es viele verwundert, dass es sich immer wieder bestätigt.

Warum gibt es kaum Ziehungen mit 37 verschieden Zahlen. Nun, der Anteil aller möglichen Permutationen von 37 Zahlen beträgt etwa ein Billiardstel aller möglichen Kombinationen (37!/37³⁷).

Eine einfache Erklärung des Gesetzes der kleinen Zahlen

Mit die Zahl der möglichen Kombinationen der Länge 37 aus 37 Zahlen ist etwas groß, um sie aufzuzählen. Deshalb versuchen wir es mit einem Würfel und den Zahlen 1 bis 6. Es gibt 6⁶ = 46.656 Kombinationen. Gibt es folgende besonderen Kombinationen mit einer EINS:

Zahl „EINSer“	Kombinationen	Wahrscheinlichkeit
6	1	0,002%
5	30	0,064%
4	375	0,804%
3	2.500	5,358%
2	9.375	20,094%
1	18.750	40,188%
0	15.625	33,490%

In etwa einem Drittel der Kombinationen der Länge sechs kommt keine EINS vor. (Hier geht es um Kombinatorik, nicht Wahrscheinlichkeit.) Dies ist (5/6)⁶. Im Roulette beträgt der Anteil (36/37)³⁷ = ~36,285%. Mit steigender Zahl der Kugeln nähert sich der Anteil dem Kehrwert der Zahl e, ~36,788%. Verallgemeinert handelt es sich um einen Grenzfall der Binominal-Verteilung, der Poisson-Verteilung.

Die Bezeichnung als (Zwei-)Drittel-Regel ist – wie man sieht – eine sehr grobe Näherung. Dieses Verhältnis als Gesetz zu bezeichnen, das die Ziehungen einhalten müssen, verkennt Ursache und Wirkung. Die Kombinationen, die keine EINS enthalten, sind in keiner Weise bevorzugt. Wenn ich ein Los aus einer Urne ziehe, die alle möglichen Kombinationen enthält, dann werde ich feststellen, dass etwa ein Drittel der Folgen auf den Losen keine EINS enthalten. Ein Drittel enthält auch keine ZWEI, ein Drittel keine DREI … Manche Lose überschneiden sich in den Eigenschaften.

Sie haben eine Permanenz beliebiger Länge vorliegen. Dann gibt es 37 Möglichkeiten diese Permanenz um eine Zahl zu erweitern. Jeder dieser 37 neuen Permanenzen hat die gleiche Wahrscheinlichkeit 1/37. Keine wird durch ein Gesetz der kleinen Zahl bevorzugt.

Gewinnstrategien, die auf dem Gesetz der kleinen Zahl basieren sind esoterischer Unfug. Alle Strategien, die auf dem Ergebnis vergangener Ziehungen beruhen, können wir streichen. Esoterischer Unfug. Basiert eine Gewinnstrategie auf dem Gesetz der kleinen Zahl, können wir sie ungesehen in den Mülleimer werfen. Sorry, Herr Onur Ünal.

Verlassen wir diesen Seitenweg und kehren zur Frage zurück, wie kann man Gewinnstrategien beweisen oder widerlegen.

Alle Permanenzen prüfen – ein aussichtsloser Versuch

Wer eine Roulette-Strategie unter das Volk bringen will, führt gerne einzelne Partien an, bei denen die Strategie erfolgreich war. Eine einzelne Party beweist jedoch nichts. Es könnte einfach Zufall sein, dass die Strategie funktioniert hat. Es ist nicht unmöglich beim Roulette zu gewinnen, es ist auch nicht unmöglich dauerhaft zu gewinnen. Letzteres ist leider extrem unwahrscheinlich. Die Bank gewinnt dauerhaft. Letzteres ist extrem wahrscheinlich. Dauerhaft heißt nicht 10 oder 20 Abende. Unter dauerhaft verstehe ich, dass die Summe aller Gewinne über Wochen, Monate und Jahre steigt und nach einer Startphase nicht mehr unter 0 fällt.

Welche Gewinnstrategien funktionieren, welche nicht?

Ich nehme die Antwort vorweg: Es funktioniert keine!

Warum dies so ist, werde ich im Folgenden erläutern. Lassen Sie mich die Betrachtungen dazu langsam und systematisch aufbauen. Bevor ich mein Geld mit einer angeblichen Gewinnstrategie riskiere, möchte ich sie gerne prüfen.

Beliebt ist die Prüfung gegen die Permanenzen einer Spielbank, die für – ausgewählte – Tische von einigen Spielbanken veröffentlicht werden. Teils kostenlos, teils gegen Geld. Diese Methode ist als Monte-Carlo-Methode oder -Simulation bekannt. Dieser Test ist natürlich besser als nichts, aber wer eine Gewinnstrategie verkaufen will, hat sie möglicherweise selbst gegen die bekannten Permanenzen getestet und optimiert. Möglicherweise liefert er die Auswertung auch gleich mit. Als verlässlicher Test sind allgemein bekannte Permanenzen ungeeignet. Dem Entwickler der Strategie dürfen die Permanenzen, gegen die seine Strategie bestehen muss, nicht bekannt sein. Aber die meisten machen sich nicht mal die Mühe. Da sie selbst wahrscheinlich wissen, dass sie nicht funktionieren suche sie nur nach Dummen, die nicht prüfen.

Ein Test gegen diese – wenigen – Permanenzen beweist meist nicht viel. Am besten erzeugen wir unsere Permanenzen selbst. Am Tisch 1 der Spielbank Bad Homburg werden pro Tag zwischen 300 und 500 Spiele gespielt. Nehmen wir an, es sind im Mittel 400 Spiele. In jedem Spiel wird eine von 37 Zahlen gezogen. Es gibt also eine endlich Anzahl Permanenzen. Nichts sollte leichter sein, eine Gewinnstrategie gegen alle möglichen Spielabläufe eines Abends zu testen. Ein schneller Computer sollte da doch reichen. Wir könnten mit einem vollständigen Test die Wirksamkeit der Strategie eindeutig beweisen oder widerlegen. Die Überlegung hat leider einen kleinen Schönheitsfehler.

Da es 37 Zahlen gibt, gibt es 37*37*37* … *37 = 37⁴⁰⁰ verschiedene Permanenzen, die alle die gleiche Wahrscheinlichkeit 1/37⁴⁰⁰ haben. 37⁴⁰⁰ ist eine Zahl mit 628 Stellen – ungefähr 1,90848884909 * 10⁶²⁷. Diese Zahl ist unvorstellbar riesig. Die Zahl der Atome im Weltall wird auf 10⁷⁸ geschätzt. Andere Schätzungen liegen bei10⁸⁰. Diese Zahl ist im Vergleich zur Zahl der möglichen Permanenzen verschwindend gering. 1 Milliarde Rechner, die eine Milliarde Permanenzen pro Sekunde testen können, hätten seit dem Urknall vor 15 Milliarden Jahren erst etwa 5*10³⁵ Permanenzen getestet. Ein extrem teurer Test, der nur die Kombinationen bis zur Länge 23 Coups abdeckt. Eine viel zu kurze Folge für die meisten Strategien. Ein vollständiger Test ist daher aussichtslos.

Was kann man also tun, um eine Gewinnstrategie zu prüfen

Da der Test aller möglichen Kombinationen – oder Permanenzen – nicht möglich ist, gibt es den theoretischen Ansatz über Modellierung und Wahrscheinlichkeitsrechnung oder einen statistischen über die Monte-Carlo-Methode. Nehmen wir zuerst die Wahrscheinlichkeitsrechnung.

Wahrscheinlichkeitsrechnung

Der Erwartungswert jedes einzelnen Coups ist negativ. Durch die Addition negativer Zahlen werden wir nie eine positive Zahl erreichen. Es kann daher keine Gewinnstrategie geben. Nur im Roulette gibt es Leute, die seit 200 Jahren das Gegenteil versuchen. Sie suchen das Perpetuum Mobile des Roulette. Sie zitieren gerne Napoléon:

Wagentrotz feiert Westerburg als „1. Roulette-Forscher der Welt, der das Ziel, den absolut sicheren Roulette-Dauergewinn, erreicht hat.“ Er habe damit verwirklicht, was Napoleon vorausgesagt hatte: „Le calcul vaincra le jeu“ – „Eines Tages wird die Berechnung das Spiel (den Zufall) besiegen.“

Quelle: http://www.gomopa.net/Pressemitteilungen.html?id=388&meldung=Casino-Verluste-durch-Gewinnsysteme

Napoleon lebte vom 15. August 1769 bis 5. Mai 1821. Angesichts der damaligen Zeit sei ihm diese Vorhersage verziehen.

Eine Ursache für die nicht versiegende Hoffnung ist das Martingalespiel, bei dem der Einsatz bei Verlust verdoppelt wird. Dem Spiel liegt die Annahme zugrunde, dass irgendwann ROT kommen muss, wenn man nur lange genug auf ROT setzt. Da wir immer am Ende eines Laufes eine Einheit gewinnen, gibt es keinen Verlust mehr. Der Erwartungswert wird positiv, obwohl er in jedem einzelnen Spiel negativ ist.

Diese Betrachtung hat einen Denkfehler. Leider kann es beliebig lange dauern, bis ROT kommt. Müssen wir das Spiel in einem Lauf abbrechen, dann fällt ein beliebig hoher Verlust an. Läufe der Länge n haben die Wahrscheinlichkeit qⁿ; n>0; 0 < q <1. Dabei steigt der Einsatz mit mit der Lauflänge bei jedem Spiel auf 2^n-1; in der Summe auf 2ⁿ-1. Und hier entsteht der Fehler bei der „Grenzwertbildung“. Wir müssen ja irgendwann gewinnen. Leider können wir nicht unendlich lange spielen, so dass der Grenzwert nie erreicht wird.

Außerdem wird hier vernachlässigt, dass der Einsatz (=Verlust) mit jedem Spiel auf das Doppelte steigt, seine Wahrscheinlichkeit aber um weniger als die Hälfte sinkt. Damit strebt der Verlust tatsächlich gegen unendlich.

Ein kurzer Ausflug in die Formelwelt der Mathematik

Der Erwartungswert bei einem Lauf der Länge n beträgt: ∑((1-q)*q^(i-1)) – qⁿ*2^(n-1) = 1 – qⁿ – qⁿ*2^(n-1) – dabei gilt: 0 < i <= n.

Für n → ∞ geht q ⁿ gegen 0 und damit der Erwartungswert der Summe gegen 1. Die gewöhnliche Argumentation endet hier. Der Ausdruck qⁿ*2^(n-1) geht jedoch für q > 0,5 gegen unendlich. Beim Roulette gilt: q=19/37 > 0,5. Und damit ist bei der Martingale der Erwartungswert für den Spieler negativ. Die Martingale ist damit keine Strategie für dauerhafte Gewinne.

Nichts neues, aber trotzdem beruhen Strategien auf dem Prinzip der Progression, der Erhöhung des Einsatzes bei Verlust. Dass die Martingale nicht funktioniert hält die Esoteriker nicht davon ab, zu versuchen, die Progression mit verschiedenen Methoden flacher zu gestalten um ein Tischlimit, der Hauptfeind der Progression, da es unter dem des eigenen Vermögens liegt, nicht zu überschreiten.

Markow-Ketten

Ich liebe endliche Automaten, Markow-Algorithmen, -ketten oder -prozesse. Viele Dinge lassen sich mit ihnen modellieren – auch Roulette-Strategien.

Hier ein Beispiel:

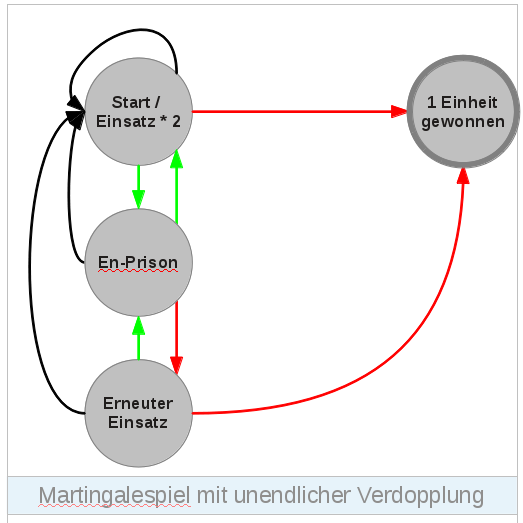
Die obige Markow-Kette modelliert ein Martingalespiel bei dem der Spieler unbegrenzt verdoppelt kann unter der Berücksichtigung der NULL. Die roten Pfeile symbolisieren die Übergänge beim Ereignis RED (p=18/37), die schwarzen Pfeile BLACK (p=18/37) und die grünen Pfeile ZERO (GREEN) (p=1/37).

Grundsätzlich muss das Verdoppeln nie enden. Die Wahrscheinlichkeit für ein Ende hat nur den Grenzwert 1. Sie ist nicht 1. Für einen Spielabbruch in endlicher Zeit ist dies tödlich. Das Spiel kann in einem Zustand mit Verlust anhalten.

Die Wahrscheinlichkeiten in einem bestimmten Zustand zu landen kann man einfach mit linearen Gleichungen berechnen, wobei jeder Knoten eine Unbekannte darstellt. Es werden nur einfache Grundrechenarten benötigt. Wollte ich damit ein Spiel modellieren, dass mit 600€ startet und maximal 400 Coups dauern darf, wird des sehr kompliziert. Es wären etwa 1000 * 400 * 10 * 2 Zustände zu berücksichtigen und es wäre eine Matrix der Größe 8 Millionen mal 8 Millionen zu lösen. Noch komplexer wird es, wenn ich mindestens 20 Spiele spielen muss und danach bei positivem Saldo vorzeitig abbrechen will. Nichts für einen simplen Taschenrechner. Auch der normale PC hat nicht so viel Speicher. Rekursive Berechnung ist auch nicht zu empfehlen. Von jedem Knoten gehen drei Möglichkeiten ab und es geht 400 Ebenen in die Tiefe. 3⁴⁰⁰ Berechnungen sind nicht durchführbar. Außerdem hätten wir dann nur eine Startbedingung durchgespielt.

Monte-Carlo-Simulation

Monte-Carlo-Simulation oder Monte-Carlo-Studie, auch MC-Simulation, ist ein Verfahren aus der Stochastik, bei dem sehr häufig durchgeführte Zufallsexperimente die Basis darstellen. Es wird dabei versucht, mit Hilfe der Wahrscheinlichkeitstheorie analytisch nicht oder nur aufwändig lösbare Probleme numerisch zu lösen.(Quelle: WikiPedia)

Da wir nicht alle Permanenzen prüfen können und eine Modellrechnung beliebig komplex bis praktisch unlösbar werden kann, versuchen wir es mit einer kleinen, handhabbaren Untermenge. Wir simulieren eine sehr große Zahl Roulette-Abende um eine Strategie zu testen. („Kleine“ und „große“ sind bei der Zahl der Möglichkeiten leichte Unter- oder Übertreibungen.) Die statistischen Ergebnisse geben eine Näherungslösung. Wenn eine Strategie diesen Test nicht besteht, wird sie auch in der Realität scheitern.

Dazu nehmen wir jedoch nicht die Permanenzen eines Spiel-Casinos. Die Zahl ist zu gering. Um mit einem statistischen Test eine unbekannte Wahrscheinlichkeit mit 95% Sicherheit auf 0,1% genau zu bestimmen, sind etwa ein Millionen Versuche erforderlich. Da der Bankvorteil bei 1,4 bzw. 2,7% liegt, kommen weniger Versuche nicht in Frage. Bei 10.000 Versuchen erreichen wir nur eine Genauigkeit von einem Prozent. In diesem Fall ist ein Ausreißer ins Plus zu wahrscheinlich.

Da es nicht genug „Permanenzen“ gibt, muss ich meine Zufallszahlen selbst erzeugen. Kein Gewinnstrategieentwickler kennt unsere Zufallsfolgen; sie werden einmalig sein. Einen Strategie kann also nicht gegen diese Zufallszahlen optimiert sein. Ein Martingalespiel für eine Millionen Abende zu simulieren dauert mit einem modernen PC keine Minute.

Ich habe mich gefragt, warum Karl-Heinz Grotelaers seine Berliner Casino Wette gewinnen konnte. Also habe ich eine Millionen Abende mit folgenden Bedingungen simuliert:

• Jeder Abend startet mit 600 Einheiten.
• Es wird nur auf einfache Chancen gesetzt.
• Es wird mit einer Einheit begonnen, und
• geht nach jedem Gewinn mit einer Einheit weiter.
• Bei Verlust wird verdoppelt,
• kann nicht mehr verdoppelt werden, wird der Rest gesetzt.
• Es müssen mindestens 20 und dürfen
• höchstens 400 Coups pro Abend gespielt werden.
• Der Abend wird beendet, wenn mehr als 20 Coups gespielt sind und der Spieler mindesten eine Einheit im Plus ist.
• Es gilt die En-Prison bei GRÜN. Der Einsatz wird mit der nächsten Kugel frei – und nochmals gesetzt – oder verloren.

Unter diesen Umständen endeten in 4 Simulationen durchschnittlich 22.046 Abende mit Verlust. Davon durchschnittlich nur 16.285 mit Totalverlust. Die Wahrscheinlichkeit für einen Abend mit Verlust liegt daher etwa bei 2,205%. Die Wahrscheinlichkeit 10 Abende nicht zu verlieren ist daher etwa 80%.

Das Verhältnis Verlust zu Umsatz lag nach einer Millionen spielen jedes Mal zwischen 1,30% und 1,38%.

Dann habe ich das Minimum der Coups auf 100 erhöht. In dieser Simulation lag das Verhältnis Verlust zu Umsatz bei 1,40%, was dem theoretischen Wert 1,388% schon recht nähe kommt. Die Zahl der verlorenen Abende steigt wegen der erhöhten Zahl der minimalen Coups pro Abend naturgemäß auf ~10,2%. (Totalverlust ~7,15%)

Da der Output ca. 210 MiByte je Simulation beträgt, erspare ich mir, die Tabelle der Abende hier zu veröffentlichen. Ich werde das „quick and dirty“ Programm noch etwas vom Dreck befreien und später veröffentlichen.

Update: Die Prüfung des Programm brachte einen kleinen Fehler bei der Behandlung des Spielendes/-abbruchs im Falle des gesperrten Einsatz bei GRÜN im letzten Coup. Hier muss die Kugel noch einmal rollen, auch wenn dadurch 401 Coups am Abend gespielt werden. Die Simulationen wurde nach der Anpassung wiederholt. Die Änderungen im Ergebnis sind vernachlässigbar.
Ende Update

Hier nur die Endergebnisse:

Mindestens 20 Coups

Coups	Umsatz	Gewinn	G/U
24.054.005	110.329.544	-1.431.887	-1.30%
24.064.081	110.472.575	-1.515.129	-1.37%
24.022.254	110.096.541	-1.492.587	-1.36%
24.041.098	110.362.145	-1.526.491	-1.38%

Mindestens 100 Coups

Coups	Umsatz	Gewinn	G/U
110.054.223	508.036.348	-6.918.733	-1.36%
110.012.906	507.705.252	-7.115.381	-1.40%
110.021.309	507.902.170	-7.199.721	-1.42%
109.969.003	507.480.478	-7.167.894	-1.41%

Eine weitere Simulation mit 10 Millionen Abenden mit mindestens 20 bzw. 100 Coups bestätigte diese Ergebnisse

Coups	Umsatz	Gewinn	G/U
240.475.632	1.103.216.300	-15.378.625	-1.39%
1.100.269.881	5.080.919.516	-71.090.369	-1.4%

Ein Martingalespiel führt zu vielen kleinen Gewinnen und wenigen großen Verlusten. Die Summe der Verluste übersteigt auf Dauer die Summe der Gewinne.

Die Simulationen bestätigen auch die Abnahme, dass in 6 von 10.000 Abenden a 400 Coups eine Zahl nicht vorkommt. In 509 von 791.909 Spielen a 400 Coups einer Simulation kam mindesten eine Zahl nicht vor. Dies sind ungefähr ~0,06428%, was dem rechnerischen Wert von 0,06434% auf einen halben Abend nahe kommt.

Ist eine flachere Progression ein Ausweg?

Ein Argument gegen ein Martingalespiel mit Verdoppeln des Einsatzes ist, dass der Einsatz extrem schnell ansteigt und das Tischlimit oder eigene Vermögen übersteigt. Um dies hinaus zu zögern wurden flachere Prognosen vorgeschlagen, bei denen der Rückgewinn dann jedoch mehre Spiele benötigt. Wie ich schon in einem früheren Artikel gezeigt habe, ist die beste Strategie ein Vermögen zu verdoppeln oder vervierfachen alles auf eine Karte zu setzen. Zwar schwebt man damit zwischen Totalverlust und Gewinn, aber die Wahrscheinlichkeit das Ziel zu erreichen ist maximal.

Dies möchte ich etwas näher untersuchen.

Wie viele Coups darf eine Gewinnstrategie umfassen?

Gerne wird davon gesprochen, dass eine Gewinnstrategie es ermöglicht, dauerhaften Gewinn zu machen und Verluste wieder auszugleichen. Grundsätzlich ist beides gleichwertig. Dauerhafter Gewinn bedingt, dass Verluste ausgeglichen werden, und der Ausgleich eines Verlustes führt dazu, dass dauerhaft Gewinn möglich sein muss. Da in jeder Gewinnstrategie das erste Spiel auch verloren gehen kann, muss sie den Verlust in den folgenden Schritten ausgleichen können.

Wir wollen daher von einer Gewinnstrategie sprechen, wenn die Strategie uns auf Dauer einen kleinen Gewinn liefert. D.h. der Erwartungswert nach einer endlichen Zahl Coups soll größer als 0 sein.

Nehmen wir an, dass die Gewinnstrategie in maximal n Schritten zum Ziel führt. Die klassische Martingale ist ein Verfahren, das erst in beliebig viel Schritten zum Gewinn führt. Alle auf Progression ausgerichteten Systeme sind nach oben offen. Dies wollen wir vorerst ignorieren.

Unsere Gewinnstrategie wird uns empfehlen im ersten Coup C1 einen bestimmten Einsatz E₁ zu setzen. Nun ist der Erwartungswert in diesem Coup negativ (-1,39% bei einfachen, -2,72% bei mehrfachen Chancen). Wir könnten unsere Strategie dadurch verbessern, dass wir nicht spielen. Wir legen unseren Einsatz E₁ zur Seite und folgen der Strategie für den Fall des Verlustes. Unsere Gewinnstrategie muss diesen Verlust -E₁ in den verbleibenden n-1 Spielen ausgleichen können.

Nun wird unsere Strategie den Einsatz E₂ für das zweite Spiel vorschlagen. Auch hier ist der Erwartungswert des einzelnen Spieles negativ. Wir können die Strategie wieder verbessern, indem wir den Einsatz E₂ zu E₁ legen und nicht spielen. Wir tun so, als hätten wir zweimal verloren. Eine Strategie, die in maximal n Schritten zum Ziel führt, muss uns diesen Einsatz auch in maximal n-2 Coups ausgleichen können. Dies können wir immer weiter treiben. Am Ende erreichen wir den letzten Coup Cn. Auch dieser hat für sich genommen einen negativen Erwartungswert und wir können unsere Strategie verbessern, indem wir den Einsatz E_n zu den vorherigen legen und nicht spielen. In diesem Fall haben wir die Gewinnstrategie um die Summe aller Einsätze verbessert. Allerdings bleiben wir im letzten Spiel auf dem gesamten Verlust sitzen, da wir auch hier nicht spielen. Dass die Strategie die Verluste in den verbleibenden 0 Coups wett machen kann, darf bezweifelt werden. Glücklicherweise heben sich unser Verlust und die zurückgelegten Einsätzen auf. Der Erwartungswert ist 0 und wir haben nicht ein Spiel gespielt. Wir hatten jedoch einen Erwartungswert größer 0 angenommen. Dies bedeutet im Umkehrschluss, dass es keine Gewinnstrategie geben kann, die in endlicher Zeit einen dauerhaften Gewinn garantiert.

Wir könnten auch umgekehrt argumentieren. Wenn eine Gewinnstrategie nach n Coups einen positiven Erwartungswert hat, dann muss sie auch in den n-1 Schritten einen positiven Erwartungswert gehabt haben, da der letzte Coup einen negativen Erwartungswert hat. Er würde das Ergebnis nur verschlechtern. Auch müsste er garantiert alle angehäuften Verluste bis zu diesem Spiel ausgleichen. Wir können die Strategie daher um den letzten Schritt kürzen. Und diese neue Strategie ebenfalls, bis wir zum ersten Spiel kommen, das aber einen negativen Erwartungswert hat.

Dies bedeutet, dass es keine Gewinnstrategie geben kann, die in endlichen Zügen einen positiven Erwartungswert liefert und dauerhaften Gewinn verspricht.

Wie sieht es mit unendlichen Coups aus. Auch hier können wir den ersten Schritt weglassen und den Einsatz zur Seite legen. Wir tun so als hätten wir verloren. Uns bleiben ja unendlich viele Coups diesen Verlust auszugleichen. So geht es auch mit dem zweiten, dritten, vierten Coup und so weiter.

Fazit

Nicht spielen gewinnt!

Oder: Es gibt keine Gewinnstrategien. Was nicht überrascht, denn die Summe negativer Erwartungswerte wird nie positiv.

Was nun?

Eigentlich wollte ich ja wissen, wie lang eine Gewinnstrategie sein darf und ob eine flachere Progression einen Ausweg darstellt. Nun ist klar, die optimale Strategie umfasst 0 Spiele. Nicht spielen. Trotzdem möchte ich den Effekt der flacheren Steigerung der Einsätze untersuchen. Wie ich in einem früheren Artikel gezeigt habe, ist es für das Ziel den Einsatz zu verdoppeln am besten, alles auf eine einfache Chance zu setzen. Eine Aufteilung auf mehrere Coups erhöht nur die Transaktionskosten, die an die Spielbank zu zahlen sind. Es kommen daher nur Satzmöglichkeiten in Frage, die den Einsatz und einen kleinen Gewinn in einem Spiel zurück bringen können.

Beim klassischen Martingalespiel setzen wir immer die Summe der bisherigen Verluste plus eine Einheit – dies ist nur eine andere Formulierung der Strategie. Mit der Wahrscheinlichkeit 18/37 gleichen wir den Verlust in einem Spiel aus und gewinnen eine Einheit. Mit der Wahrscheinlichkeit 19/37 erhöht sich der Verlust.

Die folgende Strategie habe ich der Seite Ein perfektes Roulette System entnommen und modifiziert. Das selbsternannte Genie Prof. Dr. Alexander Gabriel Friedmann preist sein System wie folgt an:

• ich vertraue Ihnen das perfekte Roulette System KOSTENLOS an
• eine durchschnittliche Gewinnchance von 98,6%
• Gewinne um die 500-750€ pro STUNDE
• Sie riskieren KEINEN Cent Ihres eigenen Geldes
• keine Angabe von persönlichen Daten oder Ihrer E-Mail Adresse
• absolut legal

Außerdem verspricht er, das 500 bis 750 € Gewinn pro Stunde keine Seltenheit wäre.

Schauen wir, was davon zu halten ist. Gespielt wird auf doppelte Chancen. Der Einsatz beginnt mit 5 Euro, ich nehme dies als ein Stück. Wir warten, bis ein Drittel 10 mal in Folge nicht gekommen ist. Das kann durchaus länger dauern. Die Wahrscheinlichkeit dafür, dass 10-mal ein beliebiges Drittel nicht kommt, liegt bei 4%. Da dieses Warten unsinnig ist, spare ich mir die Mühe es zu programmieren. Der Professor empfiehlt folgende Steigerungen des Einsatzes: 5, 10, 20, 30, 40, 50 Euro. In Einheiten sind dies 1, 2, 4, 6, 8, 10

Da haben wir schon das erste Problem. Wenn wir 50 Euro setzen müssen, haben wir schon insgesamt 105 Euro verloren. Um in die Gewinnzone zu kommen müssten wir 55 Euro setzen. Für die nachfolgenden Coups müssen wir die Strategie ergänzen, denn der Professor schweigt sich hier aus.

Wir wollen es auch mit einer doppelten Chance versuchen. Damit wir nach jedem gewonnenen Spiel immer minimal im Plus liegen, müssen wir statt der Summe der Verluste nur die Hälfte der bisherigen Verluste plus eine Einheit setzen. Die Einsätze steigen dadurch langsamer. Die Gewinnwahrscheinlichkeit sinkt auf 12/37 und wir haben den vollen Bankvorteil gegen uns.

Formulieren wir die Strategie etwas präziser:

1. Die aufgelaufen Verluste sind 0.
2. Setze die aufgerundete Hälfte der bisherigen Verluste plus eine Einheit auf eine doppelte Chance (z.B. die Zahlen „1“ bis „12“)
3. Wenn
   • gewonnen, dann gehe zu Schritt 1.
   • verloren, dann gehe zu Schritt 2.

Wichtig ist auf die nächste ganze Einheit aufzurunden, damit wir bei Gewinn ins Plus kommen. Die Folge unserer Progression lautet damit: 1, 2, 3, 4, 6, 9, 14, … und der Gewinn beträgt 2, 3, 3 , 2, 2, 3, …

Einen Vergleich zwischen der Einfachen (ohne En-Prison) und Doppelten Chancen zeigt folgende Tabelle:

	Einfache Chance				Doppelte Chance
Coup	Verlust	Einsatz	Wahrs.	Gewinn	Verlust	Einsatz	Wahrs.	Gewinn
1	0	1	48,649%	1	0	1	32,432%	2
2	1	2	24,982%	1	1	2	21,914%	3
3	3	4	12,828%	1	3	3	14,807%	3
4	7	8	6,588%	1	6	4	10,004%	2
5	15	16	3,383%	1	10	6	6,760%	2
6	31	32	1,737%	1	16	9	4,567%	2
7	63	64	0,892%	1	25	14	3,086%	3
8	127	128	0,458%	1	39	21	2,085%	3
9	255	256	0,235%	1	60	31	1,409%	2
10	511	512	0,121%	1	91	47	0,952%	3
11	1023	1024	0,062%	1	138	70	0,643%	2
12	2047	2048	0,032%	1	208	105	0,435%	2
13	4095	4096	0,016%	1	313	158	0,294%	3
14	8191	8192	0,008%	1	471	237	0,198%	3
15	16383	16384	0,004%	1	708	355	0,134%	2
16	32767	32768	0,002%	1	1063	533	0,091%	3
17	65535	65536	0,001%	1	1596	799	0,061%	2
18	131071	131072	0,001%	1	2395	1199	0,041%	3
19	262143	262144	0,000%	1	3594	1798	0,028%	2
20	524287	524288	0,000%	1	5392	2697	0,019%	2

Zwar steigt der Einsatz deutlich langsamer, aber die mittlere Länge eines Laufes steigt auch von ~2,06 auf ~3,08. Der Gewinn alterniert aufgrund der Rundungen zwischen 2 und 3 Einheiten. Es könnte sein, dass mit der zweiten Strategie die Berliner Spielbankwette leichter zu gewinnen ist, also muss eine Simulation her.

(Längere Programmierpause)

So, hier nun das nicht überraschende Ergebnis aus der Simulation einer Millionen Abende:

Coups	Umsatz	Gewinn	G/U
24.806.871	143.965.427	-3.858.941	-2,68%

Die Wahrscheinlichkleit einen Abend mit Verlust zu beenden, beträgt etwa 3,5%. Karl-Heinz Grotelears hätte damit seine Wette nur mit 70% Wahrscheinlichkeit gewonnen, womit er aber deutlich im Vorteil ist.

Wie steht es nun mit dem Versprechen Das System ist so konstruiert, dass ein Gewinn von 500 € bis 750€ pro Stunde keine Seltenheit ist. Um 100 – 150 Stücke zu gewinnen, braucht man etwa 100 – 200 Coups. (Man gewinnt jeden dritten Coup 2 bis 3 Stücke.) Ein Simulationslauf mit mindestens 200 Coups ergibt:

Coups	Umsatz	Gewinn	G/U
182.778.079	1.084.456.192	-29.325.919	-2.7%

Etwa 24.6% der Abende enden mit Verlust. Die Abende, die nicht im Verlust enden, liegen jedoch meistens zwischen 150 und 200 Stücke. Die Gewinne wiegen aber die Verluste auf Dauer nicht auf.

Genug. Zeit den Artikel zu veröffentlichen.